Ok

En poursuivant votre navigation sur ce site, vous acceptez l'utilisation de cookies. Ces derniers assurent le bon fonctionnement de nos services. En savoir plus.

Recherchez sur le site (cours, livres, Agregation, etc.)

Liens mathématiques divers

Avril 2024

D L M M J V S
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30
Syndicate this site (rss)
Syndicate this site (XML)

Catégories

19/11/2010

Arithmétique des polynômes

Section : Cours 
Avant : Anneau des polynômes 
Après : Racines des polynômes 

 

Arithmétique des polynômes

Il s'agit de répéter pour les polynômes des résultats similaires à ceux qui ont été énoncés pour les entiers.

 

Premier point à observer : l'arithmétique sur les polynômes est tout à fait analogue à celle sur les entiers à condition de travailler sur des polynômes sur un corps commutatif. Sur un anneau commutatif quelconque (même intègre) se glissent quelques bizarreries.

 

Second point à observer : les énoncés donnés sur les entiers l'ont été sur des entiers positifs. Ils se modifient sans trop de mal pour des entiers de $ mathbb{Z}$ mais parfois en s'alourdissant un peu ; ainsi dans $ mathbb{Z}$ on ne peut plus affirmer l'existence d'un entier $ d$ unique tel que $ n$ divise $ 10$ et $ 6$ si et seulement si $ n$ divise $ d$ (le pgcd de $ 10$ et $ 6$ ) : il en existe toujours un, mais il n'est plus unique, on peut prendre $ d=2$ mais aussi $ d=-2$ . Les polynômes unitaires joueront un rôle analogue aux entiers positifs mais ils sont légèrement moins confortables, dans la mesure où la somme de deux entiers positifs est positive alors que la somme de deux polynômes unitaires n'est pas nécessairement unitaire. Attention à ces petits détails donc, en apprenant les énoncés.

Commençons par donner une définition, à partir de laquelle on ne montrera guère de théorèmes que dans $ mathbb{K}[X]$ mais que ça ne coûte pas plus cher de donner sur un anneau commutatif quelconque.

 

 

Définition 9   Soit $ A$ un anneau commutatif. On dit qu'un polynôme $ P$ dans $ A[X]$ est un multiple d'un polynôme $ S$ dans $ A[X]$ , ou, de manière équivalente, que $ S$est un diviseur de $ P$ , lorsqu'il existe un polynôme $ T$ dans $ A[X]$ tel que $ P=ST$ .

 

Comme pour les entiers, tout repose sur la division euclidienne.

 

 

Théorème 1   Soit $ mathbb{K}$ un corps commutatif, $ A$ un polynôme de $ mathbb{K}[X]$ et $ B$ un polynôme non nul de $ mathbb{K}[X]$ . Il existe un couple $ (Q,R)$ unique de polynômes vérifiant la double condition :

 

$displaystyle A=QB+Rqquad{rm et}qquad deg R < deg B. $

 

 

 


Démonstration : On prouvera successivement l'existence et l'unicité de $ (Q,R)$ .

 

Existence de $ (Q,R)$

 

La preuve est significativement différente de celle utilisée pour les entiers. Elle est toujours basée sur une maximisation/minimisation, mais les polynômes n'étant pas totalement ordonnés, cette maximisation est un peu plus technique.

Dans le cas stupide où $ B$ divise $ A$ , prenons $ R=0$ et $ Q$ tel que $ A=BQ$ . Sinon, considérons l'ensemble

 

$displaystyle {mathcal R}={A-QB mid Qinmathbb{K}[X]}, $

 

qui est donc un ensemble non vide de polynômes non nuls ; puis l'ensemble

 

$displaystyle E={deg R mid Rin{cal R}}, $

 

qui est un ensemble d'entiers positifs non vide. Cet ensemble $ E$ possède donc un plus petit élément $ d$  ; prenons un $ R$ dans $ cal R$ dont le degré soit $ d$ et enfin un $ Q$ tel que $ A-QB=R$ .

Nous devons vérifier que ces choix conviennent ; l'identité entre $ A$ , $ B$ , $ Q$ et $ R$ est claire, reste l'inégalité concernant les degrés. Vérifions-la par l'absurde, en supposant que $ deg Bledeg R$  ; notons $ e$ le degré de $ B$ et

 

$displaystyle B=b_eX^e+b_{e-1}X^{e-1}+cdots+b_0,quad R=r_dX^d+r_{d-1}X^{d-1}+cdots+r_0. $

 

Posons

 

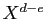
$displaystyle Q_1=Q+frac{r_d}{b_e}X^{d-e}. $

 

Remarquons qu'en écrivant cette définition, on utilise l'hypothèse $ deg Bledeg R$ , qui justifie que $ X^{d-e}$ ait un sens, et simultanément le fait qu'on travaille dans un corps, qui justifie la possibilité de diviser par $ b_e$ .

Considérons alors

 

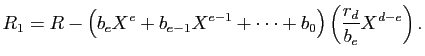
$displaystyle R_1=A-Q_1B=A-QB-left(frac{r_d}{b_e}X^{d-e}right)B, $

 

donc

 

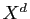
$displaystyle R_{1}= R-left(b_eX^e+b_{e-1}X^{e-1}+cdots+b_0right) left(frac{r_d}{b_e}X^{d-e}right). $

 

Dans cette dernière écriture, on voit se simplifier les termes en $ X^d$ de $ R$ et du produit qu'on lui a soustrait, et on constate donc avoir obtenu un polynôme $ R_1$ de degré strictement plus petit que celui de $ R$ . Mais alors le degré de $ R_1$ est dans $ E$ et contredit l'hypothèse de minimisation qui a fait choisir $ d$ . Contradiction !

 

Unicité de $ (Q,R)$

 

Soient $ (Q_1,R_1)$ et $ (Q_2,R_2)$ deux couples vérifiant les deux conditions exigées dans l'énoncé du théorème.

On déduit de $ A=Q_1B+R_1=Q_2B+R_2$ que $ (Q_2-Q_1)B=R_1-R_2$ . Ainsi, $ R_1-R_2$ est un multiple de $ B$ . Des conditions $ deg R_1<deg B$ et$ deg R_2<deg B$ , on déduit que $ deg(R_1-R_2)<deg B$ .

Ainsi $ R_1-R_2$ est un multiple de $ B$ de degré strictement plus petit. La seule possibilité est que $ R_1-R_2$ soit nul. On en déduit $ R_1=R_2$ , puis, en allant reprendre l'égalité $ (Q_2-Q_1)B=R_1-R_2$ , que $ Q_1=Q_2$ .$ square$

 

 

Remarque : On a choisi d'énoncer ce théorème sur un corps commutatif pour faciliter sa mémorisation et parce que l'on n'aura presque jamais besoin d'un énoncé plus général. On aura toutefois besoin une fois de l'utiliser pour des polynômes sur un anneau ; remarquons donc que la démonstration montre que le résultat reste vrai sur un anneau commutatif quelconque à condition de supposer non seulement que $ B$ est non nul, mais même que son coefficient dominant est inversible : le seul endroit où on a utilisé qu'on s'était placé dans un corps commutatif a en effet été une division par ce coefficient dominant.

 

 

Exemple 2   Concrètement, on disposera les divisions euclidiennes de polynômes comme les divisions de nombres entiers. Par exemple, pour diviser $ P=X^2+X+1$ par $ Q=X-1$ , on écrit :

 

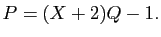
begin{displaymath} begin{array}{lvert l} begin{array}{l} X^2+X+1\ X^2-X ... ...ray}{l} X-1\ hline X+2\ \ \ \ end{array}end{array}end{displaymath}

 

Ce qui fournit la division euclidienne :

 

$displaystyle P=(X+2)Q-1. $

 

 

Nous définissons ensuite le pgcd. On ne donnera pas ici d'énoncés concernant le $ mathrm{ppcm}$ , non qu'il n'y en ait pas (ce sont là aussi les mêmes qu'en arithmétique des entiers) mais parce qu'ils ne semblent pas très importants. Les étudiants curieux les reconstitueront eux-mêmes.

 

 

Théorème 2   Soit $ mathbb{K}$ un corps commutatif. Soient $ A$ et $ B$ deux polynômes de $ mathbb{K}[X]$ . Il existe un unique polynôme unitaire $ D$ de $ mathbb{K}[X]$ tel que pour tout polynôme $ P$de $ mathbb{K}[X]$ , $ P$ divise $ A$ et $ B$ si et seulement si $ P$ divise $ D$ .

De plus il existe deux polynômes $ S$ et $ T$ de $ mathbb{K}[X]$ tels que $ D=SA+TB$ (identité de Bézout).

 

Et tant qu'on y est avant de passer aux démonstrations :

 

 

Définition 10   Le plus grand commun diviseur de deux polynômes $ A$ et $ B$ est le polynôme unitaire $ D$ apparaissant dans l'énoncé du théorème précédent.

 

 

 

Notation 7   Le plus grand commun diviseur de $ A$ et $ B$ sera noté $ mathrm{pgcd}(A,B)$ .

 

Comme pour les entiers, plusieurs démonstrations sont possibles ; on ne donne que celle basée sur l'algorithme d'Euclide.

 


Démonstration : La démonstration est une récurrence sur le degré de $ B$ .

Merveilles du copier-coller, voici de nouveau un «résumé de la preuve»  sous forme de programme informatique récursif (le même que pour l'arithmétique des entiers) :

 

Début du programme

* Pour $ B=0$ , $ mathrm{pgcd}(A,0)=A/{}$ coefficient dominant de $ A$ .

* Soit $ R$ le reste de la division euclidienne de $ A$ par $ B$ .

Les diviseurs communs de $ A$ et $ B$ sont ceux de $ B$ et $ R$ .

D'où : $ mathrm{pgcd}(A,B)=mathrm{pgcd}(B,R)$ .

Fin du programme

 

Et voici, toujours par les vertus du copier-coller, la preuve récurrente formelle. On va démontrer par «récurrence forte»  sur le degré $ d$ de $ B$ l'hypothèse $ (H_d)$ suivante :

$ (H_{d})$ Pour tout polynôme $ A$ et tout polynôme $ B$ de degré $ d$ , il existe deux polynômes $ S$ et $ T$ tels que, pour tout polynôme $ P$ , $ P$ divise $ A$ et $ B$ si et seulement si $ P$ divise $ SA+TB$ .

Vérifions $ (H_{-infty})$ .

Il s'agit donc de traiter le cas où $ B=0$ . Soit $ A$ un polynôme ; tout polynôme $ P$ qui divise $ A$ divise aussi $ B=0$ puisque $ 0P=0$ . Pour tout $ P$ , $ P$ divise $ A$ et 0 si et seulement si $ P$ divise $ A$ . Prenons alors $ S=1$ et $ T=0$  : on a donc bien pour tout $ P$  : $ P$ divise $ A$ et 0 si et seulement si $ P$ divise $ SA+Ttimes 0$ .

 

Soit $ d$ un entier fixé. Supposons la propriété $ (H_c)$ vraie pour tout $ c$ strictement inférieur à $ d$ et montrons $ (H_d)$ .

Soient $ A$ un polynôme et $ B$ un polynôme de degré $ d$ . Notons $ A=BQ+R$ la division euclidienne de $ A$ par $ B$ (qu'on peut réaliser puisque $ Bnot=0$ ).

Vérifions l'affirmation intermédiaire suivante : pour tout $ P$ , $ P$ est un diviseur commun de $ A$ et $ B$ si et seulement si $ P$ est un diviseur commun de $ B$ et $ R$ . (Avec des mots peut-être plus lisibles : «les diviseurs communs de $ A$ et $ B$ sont les mêmes que ceux de $ B$ et $ R$ »).

Soit $ P$ un diviseur commun de $ A$ et $ B$ , alors $ P$ divise aussi $ R=A-BQ$  ; réciproquement soit $ P$ un diviseur commun de $ B$ et $ R$ , alors $ P$ divise aussi $ A=BQ+R$ .

L'affirmation intermédiaire est donc démontrée.

 

On peut alors appliquer l'hypothèse de récurrence $ (H_{deg R})$ (puisque précisément $ deg R < deg B$ ) en l'appliquant au polynôme $ B$ .

On en déduit qu'il existe deux polynômes $ S_1$ et $ T_1$ tels que pour tout $ P$ , $ P$ divise $ B$ et $ R$ si et seulement si $ P$ divise $ S_1 B+T_1 R$ .

Remarquons enfin que $ S_1 B+T_1R=S_1 B+T_1(A-BQ)=T_A A+(S_1-Q)B$ , et qu'ainsi, si on pose $ S=T_A$ et $ T=S_1-Q$ on a bien prouvé que, pour tout $ P$, $ P$ divise $ Q$ et $ B$ si et seulement si $ P$ divise $ SA+TB$ .

$ (H_d)$ est donc démontrée.

 

On a donc bien prouvé $ (H_d)$ pour tout $ dinmathbb{N}cup{-infty}$ .

 

Une fois qu'on en est arrivé là, il ne reste donc plus qu'à montrer que pour un polynôme $ P$ (le polynôme $ SA+TB$ ) il existe un unique $ D$ unitaire tel que $ Q$ divise $ P$ si et seulement si $ Q$ divise $ D$ . L'existence est claire : comme le résumé le suggère, on divise $ P$ par son coefficient dominant et on obtient un polynôme $ D$ unitaire ayant les mêmes diviseurs que $ P$ . Pour ce qui est de l'unicité, elle est évidente pour $ P$ nul ; on supposera $ P$ non nul. Soit maintenant $ D_1$ un polynôme unitaire ayant exactement les mêmes diviseurs que $ P$ . Alors comme $ P$ divise $ P$ , $ P$ divise $ D_1$ , et comme $ D_1$ divise $ D_1$ , $ D_1$ divise $ P$ . Les polynômes $ P$ et $ D_1$ se divisent donc mutuellement ; soit $ Q_1$ et $ Q_2$ les quotients respectifs de $ P$ par $ D_1$ et de $ D_1$ par $ P$ . En utilisant la formule calculant le degré d'un produit, on voit que forcément, $ P$ a même degré que $ D_1$ et que les polynômes $ Q_1$ et $ Q_2$ sont de degré nul, donc des constantes $ lambda_1$ et $ lambda_2$ . Soit $ a_d$ le coefficient dominant de $ P$  ; le coefficient dominant de $ Q_1D_1=P$ vaut$ lambda_1cdot 1$ donc $ lambda_1=a_d$ et $ D_1$ est égal à $ P/$ (coefficient dominant de $ P$ ), donc à $ D$ , ce qui prouve l'unicité.$ square$

 

Nous allons ensuite définir le pgcd d'un nombre fini de polynômes. En arithmétique des entiers, cette notion n'est pas primordiale ; en revanche dans les applications des raisonnements arithmétiques à des polynômes, on est souvent dans des cas où on s'intéresse à des pgcds de plus de deux polynômes à la fois.

L'énoncé donné ci-dessus pour deux polynômes se généralise à un nombre fini, par récurrence sur ce nombre.

 

 

Proposition 9   Soit $ mathbb{K}$ un corps commutatif, $ nge1$ un entier et $ A_{1}$ , $ A_{2}$ , ..., $ A_{n}$ des polynômes de $ mathbb{K}[X]$ . Il existe un unique polynôme unitaire $ D$ de $ mathbb{K}[X]$ tel que pour tout $ P$ dans $ mathbb{K}[X]$ , $ P$ divise tous les $ A_{i}$ de $ i=1$ à $ i=n$ si et seulement si $ P$ divise $ D$ .

De plus il existe $ n$ polynômes $ S_1,ldots,S_n$ tels que

 

$displaystyle D=S_1A_1+S_2A_2+cdots+S_nA_n $

 

(identité de Bézout).

 

 


Démonstration : C'est une récurrence facile sur $ n$ . Le cas $ n=2$ est l'objet du théorème précédent (et le cas $ n=1$ a été traité dans sa démonstration, ou on peut le ramener fictivement à $ n=2$ en disant que les diviseurs de $ A_1$ sont les diviseurs communs de $ A_1$ et de 0 ).

Soit $ nge 2$ fixé, supposons la proposition vraie pour tout ensemble de $ n$ polynômes. Prenons $ n+1$ polynômes $ A_1,A_2,ldots,A_{n+1}$ . Notons $ B$ le pgcd des $ n$ premiers, qui existe par l'hypothèse de récurrence. Alors les diviseurs communs de $ A_1$ , $ A_2$ , $ ldots$ , $ A_{n+1}$ sont les diviseurs communs de $ B$ et de $ A_{n+1}$  ; donc prendre$ D=mathrm{pgcd}(B,A_{n+1})$ répond à la question. L'unicité est claire : si $ D_1$ répondait aussi à la question, les diviseurs de $ D_1$ seraient exactement les mêmes que ceux de $ D$avec $ D$ et $ D_1$ tous deux unitaires, et comme dans la preuve du théorème précédent (ou en appliquant le théorème précédent à $ D$ et 0 ), on conclut que $ D=D_1$ . La relation de Bézout est aussi le résultat d'une récurrence immédiate : il existe $ S_1,S_2,ldots,S_n$ tels que $ B=S_1A_1+S_2A_2+cdots+S_nA_n$ et $ T_1$ et $ T_2$ tels que$ D=T_1B+T_2A_{n+1}$ donc

 

$displaystyle D=(T_1S_1)A_1+(T_1S_2)A_2+cdots+(T_1S_n)A_n+T_2A_{n+1}. $

 

$ square$

 

 

 

Définition 11   Soit $ mathbb{K}$ un corps commutatif et $ nge1$ un entier. On dira que $ n$ polynômes de $ mathbb{K}[X]$ sont premiers entre eux lorsque leurs seuls diviseurs communs sont constants (en d'autres termes, quand leur $ mathrm{pgcd}$ est $ 1$ ).

 

On prendra garde à ne pas confondre «premiers entre eux»  (on dit parfois «premiers entre eux dans leur ensemble») et «deux à deux premiers entre eux»  : dans $ mathbb{R}[X]$ , les polynômes

 

$displaystyle (X-1)(X-2);,quad(X-1)(X-3);,quad (X-2)(X-3) $

 

sont premiers entre eux (dans leur ensemble) mais ils ne sont pas deux à deux premiers entre eux.

Les polynômes irréductibles sont les analogues des nombres premiers. Toutefois les usages étant ce qu'ils sont, il y a une petite nuance de vocabulaire un peu désagréable : alors que le mot «nombre premier»  est réservé à des entiers positifs, le mot «polynôme irréductible»  n'est pas réservé à des polynômes unitaires. On se méfiera de cette peu perceptible nuance qui crée de légères discordances entre énoncés analogues portant les uns sur les polynômes et les autres sur les entiers.

 

 

Définition 12   Soit $ mathbb{K}$ un corps commutatif. On dira qu'un polynôme $ P$ dans $ mathbb{K}[X]$ est irréductible lorsqu'il possède exactement deux diviseurs unitaires.

 

On remarquera tout de suite que ces deux diviseurs unitaires sont alors forcément les polynômes $ 1$ et $ P/$ (coefficient dominant de $ P$ ).

La proposition suivante est évidente, mais donne un exemple fondamental de polynômes irréductibles :

 

 

Proposition 10   Soit $ mathbb{K}$ un corps commutatif. Dans $ mathbb{K}[X]$ , les polynômes du premier degré sont irréductibles.

 

 


Démonstration : Soit $ P=aX+b$ avec $ anot=0$ un polynôme du premier degré dans $ mathbb{K}[X]$ . Cherchons ses diviseurs unitaires. Un diviseur de $ P$ doit avoir un degré inférieur ou égal à celui de $ P$ . Le seul diviseur unitaire constant de $ P$ est le seul polynôme constant unitaire : la constante $ 1$ . Cherchons les diviseurs unitaires de la forme $ X+c$ de $ P$ . Si $ X+c$ divise $ P$ , il existe un polynôme $ Q$ tel que $ P=(X+c)Q$ et en comparant les degrés, $ Q$ est nécessairement constant. 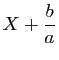En comparant les coefficients dominants, nécessairement $ Q=a$ donc $ c=displaystylefrac{b}{a}$ . 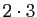Ainsi $ P$ possède exactement un diviseur unitaire du premier degré, le polynôme $ X+displaystylefrac{b}{a}$ . Le polynôme $ P$est donc irréductible.$ square$

 

Sur un corps quelconque, déterminer quels polynômes sont irréductibles et lesquels ne le sont pas est un problème très sérieux ; dans quelques pages, nous verrons que ce problème a une solution simple dans les cas particuliers des polynômes à coefficients complexes ou réels.

 

Le résultat fondamental est, comme en arithmétique entière, l'existence et unicité de la décomposition en facteurs irréductibles. Elle repose là encore sur le «lemme de Gauss». On ne réécrit pas les démonstrations pour deux raisons totalement contradictoires : d'abord parce que ce sont exactement les mêmes, et ensuite parce que ce ne sont pas exactement les mêmes -une petite difficulté se pose pour énoncer l'unicité de la décomposition en facteurs irréductibles d'un polynôme. Pour des entiers, on a convenu de classer les facteurs dans l'ordre croissant : ainsi $ 6$ se décompose en $ 2cdot 3$ et non en $ 3cdot 2$ . Une telle convention ne peut être appliquée pour décomposer des polynômes, aucun ordre «raisonnable»  n'étant à notre disposition sur l'ensemble des polynômes irréductibles ; ainsi dans $ mathbb{C}[X]$ peut-on écrire selon la fantaisie du moment$ X^2+1=(X-mathrm{i})(X+mathrm{i})$ ou $ X^2+1=(X+mathrm{i})(X-mathrm{i})$ . Quand on énonce ci-dessous que la décomposition est «unique»  on sous-entend donc qu'on considère les deux exemples qui précèdent comme la même décomposition, ce qui peut s'énoncer rigoureusement mais lourdement. Voulant glisser sur ce détail, on se condamne à rester un peu vaseux.

 

Voici donc le lemme de Gauss.

 

 

Lemme 2   Soit $ mathbb{K}$ un corps commutatif. Soient $ A$ , $ B$ et $ C$ trois polynômes de $ mathbb{K}[X]$ . Si $ A$ divise $ BC$ et est premier avec $ C$ , alors $ A$ divise $ B$ .

 

 


Démonstration : La même que pour les entiers, avec des majuscules.$ square$

 

Et voici le théorème de décomposition en facteurs irréductibles.

 

 

Théorème 3 (Énoncé moyennement précis)   Soit $ mathbb{K}$ un corps commutatif. 
Tout polynôme $ P$ non nul de $ mathbb{K}[X]$ peut s'écrire de façon «unique»  en produit :

 

$displaystyle P=lambda P_1^{alpha_1}P_2^{alpha_2}cdots P_k^{alpha_k}, $

 

dans lequel $ lambda$ est le coefficient dominant de $ P$ , les $ P_i$ pour $ 1le ile k$ sont des polynômes irréductibles unitaires deux à deux distincts, et les $ alpha_i$ sont des entiers strictement positifs.

 

 


Démonstration : À peu près la même que pour les entiers, avec un peu plus de soin pour l'unicité.$ square$

 

 




Section : Cours 
Avant : Anneau des polynômes 
Après : Racines des polynômes 


          © UJF Grenoble, 2007  

Source : http://ljk.imag.fr/membres/Bernard.Ycart/mel/pf/node4.html

19:21 Publié dans Arithmétique des polynômes | Lien permanent | Commentaires (0) | |  del.icio.us | | Digg! Digg |  Facebook

Arithmétique des polynômes

Arithmétique des polynômes

(Redirigé depuis Polynôme irréductible)

En algèbre, l'arithmétique des polynômes décrit les propriétés des polynômes qui peuvent se déduire de l'arithmétique et qui sont un peu analogues à celles des nombres entiers. Par exemple, l'anneau des polynômes K[X] à une indéterminée X et à coefficients dans un corps commutatif K dispose d'une division euclidienne. Si le lecteur n'est pas familier avec les structures de corps et d'anneau, il peut considérer K comme une lettre symbolisant l'ensemble des nombres réels ou complexes. La division euclidienne est à l'origine des théorèmes clés de l'arithmétique élémentaire. Il en est de même pour l'arithmétique des polynômes. On démontre de la même manière l'identité de Bézout, le lemme d'Euclide ou un équivalent duthéorème fondamental de l'arithmétique, les polynômes irréductibles et unitaires prenant alors la place des nombres premiers.

Ces résultats ne s'appliquent plus de la même manière si les coefficients sont choisis dans un ensemble A comme celui des nombres entiers, où les éléments ne sont pas toujours inversibles pour la multiplication. L'étude de cette configuration demande l'usage d'un attirail d'outils mathématiques plus puissants. Ils permettent de montrer que si l'identité de Bézout n'est plus vérifiée, un équivalent du théorème fondamental de l'arithmétique reste encore valable. Cette propriété reste vraie si l'anneau comporte plusieurs indéterminées. Autrement dit, si A est un anneau factoriel, l'anneau des polynômes à coefficients dans A est aussi factoriel, quel que soit le nombre d'indéterminées. Dans certains cas, l'anneau A n'est pas factoriel mais juste noethérien. À condition que l'anneau des polynômes ne contienne qu'un nombre fini d'indéterminées, il est aussi noethérien.

Ces différents résultats sont à l'origine de théorèmes fondateurs de diverses branches de l'algèbre. La théorie de Galois s'appuie sur la structure euclidienne de K[X], la théorie algébrique des nombres fait usage du caractère factoriel et noethérien d'un anneau de polynômes à une ou plusieurs indéterminées sur un anneau factoriel. Enfin, des théorèmes comme celui de la base de Hilbert ou le Nullstellensatz, essentiels en géométrie algébrique, sont des conséquences directes de l'arithmétique des polynômes.

Sommaire

 [masquer]

Corps commutatif [modifier]

Dans le reste de l'article K désigne un corps commutatif. Ce corps peut être égal à Q celui des nombres rationnels, R celui des réels ou C pour les complexes, ou encore un corps fini. Dans ce paragraphe tous les polynômes sont en une indéterminée et à coefficients dans K, l'anneau de ces polynômes est noté K[X]. L'anneau K[X] possède une division euclidienne (cf l'article Division d'un polynôme) et comme pour tout anneau euclidien, les conséquences sont multiples. Elles sont exactement semblables à celle traitées dans l'article arithmétique élémentaire, qui traite de l'arithmétique des nombres entiers.

Il est possible d'exprimer ces résultats sous deux formes, la première et la plus simple est celle utilisé dans l'article arithmétique élémentaire. La deuxième, emploie le vocabulaire de lathéorie des anneaux, c'est-à-dire des termes comme idéal, idéal principal, premier ou encore maximal. L'article explicite les résultats dans les deux langages.

Identité de Bézout [modifier]

Suivre le plan de l'article Arithmétique élémentaire, suppose dans une premier temps de s'intéresser aux sous-ensembles de K[X] non vide et stable pour l'addition et la soustraction. Pour que les conséquences soient aussi riche que dans l'article sur les entiers, il est nécessaire d'ajouter la stabilité de l'ensemble par multiplication par un polynôme quelconque. On obtient le résultat suivant :

Sous-ensemble stable — Un sous-ensemble M non vide de K[X] est stable par addition, soustraction et multiplication par un polynôme quelconque si, et seulement si, il existe un polynôme m tel que M soit l'ensemble des multiples de m.

En termes de théorie des anneaux, ce résultat indique que K[X] est un anneau principal, ce qui est le cas de tout anneau euclidien. La démonstration se trouve dans l'article Anneau euclidien.

La conséquence directe est :

Identité de Bézout — Soit P et Q deux polynômes, P et Q sont premiers entre eux si, et seulement si, il existe deux polynômes M et N tel que :

Pcdot M + Qcdot N = 1

Il devient nécessaire de définir l'expression polynômes premiers entre eux. Deux polynômes sont premiers entre eux lorsque les seuls polynômes qui les divisent tous les deux sont les polynômes constants non nuls. Cette définition est très proche de celle des entiers qui sont premiers entre eux lorsque les seuls diviseurs communs sont 1 et -1, c'est-à-dire les éléments inversibles de l'anneau.

Dans le vocabulaire des anneaux, l'identité se traduit un peu différemment. Soit A et B deux idéaux de K[X], si l'intersection de A et de B est égal au produit des idéaux A.B (ce qui est l'équivalent de l'expression premiers entre eux), alors l'idéal A + B est égal à K[X].

Polynôme irréductible [modifier]

Continuer l'analogie avec l'arithmétique élémentaire demande à ce niveau de disposer d'un équivalent des nombres premiers. Dans Z, un nombre premier n'est divisible que par 1, -1 ou le produit d'un de ces deux éléments et de lui-même. Cependant ces nombres ne sont que qualifiés d'irréductibles. Pour qu'ils soient déclarés premiers il faut en plus qu'ils soient positifs. Ce qui caractérise un nombre premier, ce sont ces multiples, or 2 et -2 ont le même ensemble de multiples, ce qui forme une classe d'équivalence dont la relation R est définie par : a et équivalent à b lorsque a et b possèdent le même ensemble de multiples. Dans le cas général, deux éléments d'un anneau a et b sont équivalents, ou encore ont le même ensemble de multiples, s'il existe un élément c inversible pour la multiplication, tel que a.c = b. Dans Z, les deux seuls éléments inversibles sont 1 et -1. On dit qu'ils sont éléments du groupe des unités et les éléments inversibles sont dits des unités. La relation d'équivalence est étudiée dans l'article Groupe des unités. Dans le cas des polynômes :

Groupe des unités de K[X] — Le groupe des unités de K[X] est formé par les polynômes constants non nuls.

On en déduit une définition pour les polynômes, presque équivalente à celle des nombres premiers :

Polynôme irréductible — Un polynôme est dit irréductible lorsqu'il n'est pas inversible et que ses diviseurs sont, soit des polynômes constants inversibles, soit le produit de lui-même par un polynôme constant.

On dispose, par exemple de la proposition :

Polynôme du premier degré — Un polynôme du premier degré est toujours irréductible.

Pour exprimer l'équivalent théorème fondamental de l'arithmétique, il est important de choisir un unique nombre premier dans chaque classe d'équivalence, pour la relation R, de nombres irréductibles. Dans Z, il suffit d'indiquer qu'un nombre irréductible est dit premier s'il est positif, car chaque classe d'équivalence contient deux éléments : a et son opposé -a. La même relation d'équivalence dans K[X] existe et la classe d'équivalence d'un polynôme P est l'ensemble des polynômes k.P si k décrit tous les éléments de K non nuls. Pour exprimer l'équivalent du théorème fondamental de l'arithmétique, on choisit généralement l'élément de la classe qui est unitaire, c'est-à-dire celui dont le coefficient du monôme dominant (celui du plus haut degré) est égal à 1. Dans chaque classe d'équivalence de polynôme irréductible, il n'existe en effet qu'un unique polynôme unitaire.

Théorème fondamental de l'arithmétique [modifier]

Article détaillé : théorème fondamental de l'arithmétique.

Avant d'énoncer le théorème fondamental, un premier lemme est utile :

Lemme d'Euclide — Soit P un polynôme irréductible et A, B deux polynômes. Si le produit des deux polynômes A.B est un multiple de P, alors soit A soit B est un multiple de P.

En termes d'anneau, ce résultat s'exprime comme par : Si un idéal premier I contient le produit de deux idéaux A et B il est contient soit A soit B , proposition toujours vraie dans unanneau principal (cf l'article Idéal premier).

On obtient finalement le théorème suivant :

Décomposition en facteurs irréductibles — Un polynôme non nul se décompose de manière unique, à l'ordre près, en un produit comportant un polynôme constant et des polynômes unitaires irréductibles.

Autrement dit, en termes d'anneau, K[X] est factoriel, car tout anneau principal est factoriel (cf l'article Anneau factoriel).

Arithmétique modulaire [modifier]

Article détaillé : Arithmétique modulaire.

Une structure digne d'intérêt sur les entiers est celle du quotient Z/nZ. Un élément de ce quotient est représenté par un reste de division euclidienne d'un entier quelconque par n, on trouve toujours un représentant unique d'une congruence modulo n dans les entiers positifs strictement plus petit que n. Si p est un entier irréductible (c'est-à-dire un nombre premier ou son opposé), la structure Z/pZ est un corps, autrement dit, tout élément non nul de Z/pZ est inversible.

Soit P un polynôme irréductible, il est tentant de considérer les polynômes de K[X] modulo P. On obtient une structure avec une addition et une multiplication, qui vérifie toutes les propriétés d'un anneau commutatif unitaire, exactement comme celle décrite dans l'article Congruence sur les entiers. On dispose encore de la propriété :

Congruence sur K[X] modulo un polynôme irréductible —  Si P est un polynôme irréductible de K[X], toute congruence modulo P non nul possède un inverse pour la multiplication.

Notons L la structure des congruences sur les polynômes de K[X] modulo P. Comme tout élément différent de 0 est inversible pour la multiplication, on dit que c'est un corps. Il est appelé le corps de rupture de K. Ce corps dispose d'une propriété remarquable :

Corps de congruence, vu comme un espace vectoriel — Le corps L dispose d'une structure de K espace vectoriel de dimension le degré de P.

Usages de l'arithmétique de K[X] [modifier]

Extension finie de R [modifier]

Article détaillé : Théorème fondamental de l'algèbre.

Le corps des complexes C peut être vu comme un espace vectoriel de dimension 2, sur R. On peut se demander s'il existe d'autres corps commutatifs contenant R. Il existe par exemple le corps des fractions rationnelles à coefficients dans R. Mais, à la différence de C, vu comme un espace vectoriel sur R, le corps des fractions n'est pas de dimension finie. Un corps commutatif contenant R et espace vectoriel de dimension finie est dit une extension finie de R. L'arithmétique des polynômes à coefficients dans R permet d'établir le résultat suivant :

Extension finie de R — Il n'existe que deux extensions finies de R : R et C, à un isomorphisme près.

L'expression un isomorphisme près signifie que si L est une extension finie de R, alors soit L est égal à R soit L est une copie de C et il existe une bijection φ de C dans L tel que l'image de R soit R et que l'addition et la multiplication soit respectées par φ, autrement dit :

forall a,b in mathbb C quad varphi (a+b) = varphi(a) + varphi(b) quadtext{et}quad varphi(acdot b) = varphi(a)cdot varphi(b)

Ce qui signifie que φ(a) est une autre manière de noter a, mais que les opérations restent strictement les mêmes.

Équation algébrique [modifier]

Article détaillé : Corps de décomposition.

L'arithmétique modulaire sur les polynômes apporte la structure de base d'une des branches de la théorie des équations, dont l'unique objet est la résolution des équations polynômiale. Soit P un polynôme à coefficients dans un corps K de degré supérieur ou égal à 1, on recherche un corps L contenant les racines de P.

Corps de décomposition — Il existe un corps L, contenant K dimension finie et contenant toutes les racines de P.

La plus petite extension vérifiant cette propriété est appelé corps de décomposition du polynôme P. Ce corps est un des ingrédients utilisé dans le cadre de la théorie de Galois pour déterminer exactement quelle équation polynômiale est résoluble par radicaux (cf l'article Théorème d'Abel (algèbre)).

Corps fini [modifier]

Article détaillé : corps fini.

Les congruences sur les anneaux sont la méthode principale d'étude des corps finis. Pour l'illustrer, considérons un nombre premier p strictement supérieur à 2 et recherchons un corps fini à p2 éléments. On considère dans un premier temps le corps Fp à p éléments, isomorphe à Z/pZ. Dans ce corps, la fonction polynôme, qui à x associe x2, n'est pas injective car x et -x ont la même image. Une application d'un ensemble fini dans lui-même qui n'est pas injective n'est pas surjective, et il existe une valeur a de Fp tel que le polynôme Pa égal à X2 - asoit irréductible.

Les congruences des polynômes de Fp modulo Pa forment un corps car Pa est irréductible. Si χ représente la classe de X modulo Pa, comme toute congruence possède comme représentant un polynôme de degré inférieur ou égal à 1, tout élément du corps des congruences est de la forme a + b.χ, avec a et b élément de Fp. On obtient bien un corps à p2éléments.

L'article détaillé montre qu'il n'existe pas d'autres corps à p2 éléments à un isomorphisme près. Cette méthode se généralise et permet de construire tous les corps finis.

Anneau factoriel [modifier]

Dans ce paragraphe A désigne un anneau factoriel, c'est-à-dire aussi non nul, commutatif unitaire et intègre. L'article Construction de l'anneau des polynômes montre que A[X] est toujours commutatif unitaire et intègre, cependant il n'est euclidien que si A est un corps (cf l'article Division d'un polynôme).

Lemme de Gauss [modifier]

Article détaillé : Lemme de Gauss (polynômes).

Cette fois ci, le groupe des unités de A[X] est plus restreint, il ne contient que les polynômes constants dont la constante est inversible dans A. Ainsi dans Z[X], l'anneau des polynômes à coefficients entiers les deux seuls polynômes inversibles sont 1 et -1. Dans ce cas, un polynôme constant non nul n'est pas nécessairement irréductible et le polynôme 6n'est plus irréductible car il est égal à 2x3. Pour cette raison, on dit qu'un polynôme est primitif lorsque ses coefficients sont premiers entre eux dans leur ensemble. Comme A est un anneau commutatif unitaire et intègre, il est possible de construire son corps des fractions K, de la même manière que l'on construit Q le corps des fractions des entiers naturels. Un polynôme P de A[X] peut aussi être considéré comme un polynôme à coefficients dans K.

On dispose d'une première propriété, appelée lemme de Gauss uniquement dans le cas où l'anneau est égal à Z, mais vraie dans tous les anneaux factoriels :

Lemme de Gauss — Un polynôme de A[X] est irréductible si, et seulement si, il est primitif et irréductible dans K[X].

Pour montrer qu'un polynôme est irréductible dans Z[X], il suffit de vérifier que ses différents coefficients ne comportent aucun facteur commun et qu'il est irréductible dans Q[X].

Les démonstrations sont proposées dans l'article Anneau factoriel.

Théorème [modifier]

Article détaillé : Anneau factoriel.

Une conséquence de ce lemme est le théorème :

Anneau factoriel — L'anneau A[X] est factoriel.

L'équivalent du théorème fondamental de l'arithmétique est encore valable, au même titre que le lemme d'Euclide, mais l'identité de Bézout n'est plus vraie et l'anneau des polynômes n'est pas principal. Pour s'en rendre compte, on peut, par exemple considérer l'idéal engendré par l'indéterminée X et a, un élément non inversible de l'anneau A, il n'est pas principal. En conséquence, il n'existe pas de polynômes N et M de A[X] tel que N.X + a.M soit égal au polynôme constant 1, même si a et X sont deux polynômes premiers entre eux. Comme l'anneau n'est pas principal, il ne peut exister de division euclidienne.

Les démonstrations sont proposées dans l'article détaillé.

Usages de l'arithmétique de A[X] [modifier]

Ces propriétés permettent parfois d'étudier la décomposition en facteurs premiers dans Q[X]. C'est le cas pour l'étude du polynôme cyclotomique, le lemme de Gauss permet de montrer que les facteurs irréductibles sont à coefficients dans Z, il devient possible de quotienter Z, l'anneau des coefficients, par p.Z où p est un nombre premier, et de conclure sur l'expression exacte des facteurs irréductibles des polynômes de la forme Xn - 1. Le lemme de Gauss peut être aussi utilisé pour démontrer le critère d'Eisenstein sur les polynômes à coefficients dans Z.

Une autre conséquence influe sur l'étude de la géométrie algébrique. Cette branche des mathématiques porte sur l'étude des variétés définies comme intersections des racines d'une famille (Pk) de polynômes en un nombre fini d'indéterminées sur un corps K. L'anneau K[X1, X2] est isomorphe à l'anneau de polynômes en une indéterminée à coefficients dans K[X1], qui est factoriel. Il est donc factoriel et une récurrence montre que K[X1, ..., Xn] l'est aussi.

Une variété algébrique peut encore être vue comme l'ensemble des points qui s'annulent sur l'idéal engendré la famille (Pk). Le caractère factoriel de l'anneau offre immédiatement des théorèmes sur les idéaux de l'anneau, offrant ainsi deux axes d'analyse, géométrique en étudiant la variété et algébrique en étudiant l'idéal. Le théorème de la base de Hilbert et leNullstellensatz sont deux résultats géométriques sur les variétés qui découlent de l'étude de la structure des idéaux.

Voir aussi [modifier]

Liens externes [modifier]

Références [modifier]

Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808)[détail des éditions]
P. Tauvel Algèbre Agrégation, Licence 3e année Dunod (2005) (ISBN 2100494120)
D. Perrin Cours d'algèbre Ellipses Marketing (1998) (ISBN 2729855521)

19:14 Publié dans Arithmétique des polynômes | Lien permanent | Commentaires (0) | |  del.icio.us | | Digg! Digg |  Facebook