21/11/2015
A Ramsey Problem on Hypercubes
A Ramsey Problem on Hypercubes
Consider the vertex set of the unit n-dimensional cube embedded in n-dimensional Euclidean space. Join each pair of vertices by a straight line segment, creating a complete graph. Color the edges of this complete graph in two colors. Graham and Rothschild proved that if n is sufficently large, there is a monochromatic complete graph of order 4 in some plane. They posed the problem of determining how large n must be. Their lower bound was 6 and their upper bound came to be known as Graham's number. Below we give links to colorings that improve the lower bound to 11. In the coloring matrices, we use colors 0 and 1.
The following link points to a coloring matrix for n=10 wherein 1/3 of the edges are bicolored. When an edge is bicolored, it can belong to cliques of either color. The matrix is here. Here, we use colors 1 and 2. An entry of 3 indicates a bicolored edge. This topic is discussed in a paper that appeared in the Journal of Discrete and Computational Geometry.
Geoff Exoo
Source :
http://isu.indstate.edu/ge/GEOMETRY/cubes.html
21:05 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Peter Cameron (mathématicien)
Peter Cameron (mathématicien)
| Naissance | Toowoomba, Queensland(Australie) |
|---|---|
| Domicile | Oxford |
| Nationalité | |
| Champs | Mathématiques |
| Institutions | Université d'Oxford Queen Mary, University of London (en) |
| Diplôme | Université du Queensland Université d'Oxford |
| Distinctions | Prix Whitehead (1979) Médaille Euler (2003) |
Peter Jephson Cameron (né le ) est un mathématicien australien qui a travaillé en théorie des groupes, encombinatoire, sur la théorie des codes, et la théorie des modèles. Il est actuellement professeur de mathématiques àQueen Mary, University of London (en).
Cameron a reçu un B.Sc. à l'université du Queensland et un D.Phil. en 1971 à l'université d'Oxford, sous la direction dePeter Neumann (de).
Œuvre[modifier | modifier le code]
Cameron s'est spécialisé en algèbre et en combinatoire ; il a écrit des livres sur la combinatoire, l'algèbre, les groupes de permutations, et la logique, et a produit plus de 250 articles1. Il a un nombre d'Erdős de 12. Son nom est attaché à laconjecture de Cameron–Erdős (en).
Bibliographie[modifier | modifier le code]
- Permutation Groups, CUP, 1999
- Combinatorics: topics, techniques, algorithms, CUP, 1994
- Sets, logics and combinatorics, Springer 1999
- Oligomorphic permutation groups, CUP, 1990 (ISBN 0521388368)
- Introduction to Algebra, Oxford University Press 1989, 2. éd. 2008
- avec Jacobus van Lint (de) : Graph theory, coding theory and block designs, CUP, 1975
- avec Jacobus van Lint : Graphs, codes and designs, CUP, 1980
- Parallelisms of complete designs, CUP, 1976
Distinctions[modifier | modifier le code]
- 1979 : Prix Whitehead
- 2003 : Médaille Euler
Notes et références[modifier | modifier le code]
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Peter Cameron » (voir la liste des auteurs).
Liens externes[modifier | modifier le code]
- Notices d’autorité : Fichier d’autorité international virtuel • International Standard Name Identifier • Bibliothèque nationale de France •Système universitaire de documentation • Bibliothèque du Congrès • Gemeinsame Normdatei • WorldCat
- (en) Peter Cameron's home page
- (en) Peter Cameron's 60th birthday conference
- (en) Theorems by Peter Cameron at Theorem of the Day
- (en) Peter Cameron's blog
- (en) Peter J. Cameron sur le site du Mathematics Genealogy Project
Source : wikipedia
21:04 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Conjecture de Cameron-Erdős
Conjecture de Cameron-Erdős
En combinatoire, la conjecture de Cameron-Erdős est l'énoncé selon lequel le nombre d'ensembles sans somme contenus dans l'ensemble {1, … , N} est O(2N/2).
Comme la somme de deux entiers impairs est un entier pair, un ensemble d'entiers impairs est toujours sans somme. Il y a ⎡N/2⎤ entiers impairs inférieurs ou égaux à N, et il y a donc 2N/2 sous-ensembles de nombres impairs dans {1, … , N}. La conjecture de Cameron-Erdős affirme que ceci compte le nombre d'ensembles sans somme, à une constante multiplicative près.
La conjecture a été formulée par Peter J. Cameron et Paul Erdős en 19881. Elle a été démontrée par Ben Green2 et indépendamment par Alexander Sapozhenko3. Sapozhenko4 donne une borne plus précise : le nombre de sous-ensembles sans somme est ∼ c0 2N/2 si N est pair, et ∼ c1 2N/2 si N est impair, où c0 et c1 sont des constantes.
Voir aussi[modifier | modifier le code]
Références[modifier | modifier le code]
- Peter J. Cameron et Paul Erdős, « On the number of sets of integers with various properties », dans R. A. Mullin (éditeur), Number Theory : Proceedings of the First Conference of the Canadian Number Theory Association (Banff, 1988), Berlin, de Gruyter, , p. 61-79
- Ben Green, « The Cameron–Erdős conjecture [archive] », Bulletin of the London Mathematical Society, vol. 36, , p. 769-778 (DOI 10.1112/S0024609304003650, arXiv math.NT/0304058)
- Alexander A. Sapozhenko, « The Cameron-Erdős conjecture », Doklady Akademii Nauk, vol. 393, no 6, , p. 749–752.
- Alexander A. Sapozhenko, « The Cameron–Erdős conjecture », Discrete Mathematics, vol. 308, no 19, , p. 4361-4369 (DOI 10.1016/j.disc.2007.08.103)
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Cameron–Erdős conjecture » (voir la liste des auteurs).
Source : wikipedia
21:03 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Conjecture d'Erdős
Conjecture d'Erdős
Le mathématicien Paul Erdős et ses nombreux collaborateurs ont émis de nombreuses et parfois fameuses conjectures mathématiques sur un large spectre de sujets.
Voici quelques-unes de ces conjectures :
- La conjecture de Cameron-Erdős sur des ensembles d'entiers ne contenant pas de somme, démontrée par Ben J. Green.
- La conjecture d'Erdős-Burr sur les nombres de Ramsey de graphes.
- La conjecture d'Erdős-Faber-Lovász (en) sur la coloration d'unions de cliques.
- La conjecture d'Erdős-Graham sur la représentation de l'unité par des fractions égytiennes monochromatiques.
- La conjecture d'Erdős-Gyárfás (en) sur les cycles dont la longueur est une puissance de 2 dans des graphes de degré minimum 3.
- La conjecture d'Erdős-Hajnal (en) selon laquelle, dans une famille de graphes définie par un sous-graphe induit exclu, chaque graphe possède soit une grande clique, soit un grand sous-ensemble indépendant. (Dans : Ramsey-type theorems, Discrete Applied Mathematics 25 (1989) 37-52)
- La conjecture d'Erdős-Heilbronn, en théorie combinatoire des nombres, minorant le nombre de sommes de deux éléments distincts d'un ensemble de résidus modulo un nombre premier, démontrée en 1994 par José António Dias da Silva et Yahya Ould Hamidoune (1947-2011).
- La conjecture d'Erdős-Lovász sur les delta-systèmes faibles-forts, ([1], p. 406), démontrée par Michel Deza (en).
- La conjecture d'Erdős-Mollin-Walsh sur les triplets consécutifs de nombres puissants.
- La conjecture d'Erdős-Menger conjecture sur les chemins disjoints dans des graphes infinis. (résolue par Ron Aharoni (en) et Eli Berger)
- La conjecture d'Erdős-Selfridge selon laquelle tout système couvrant contient au moins un module pair.
- La conjecture d'Erdős-Stewart sur l'équation diophantienne
 , démontrée par Florian Luca, (lien Math Reviews).
, démontrée par Florian Luca, (lien Math Reviews). - La conjecture d'Erdős-Straus sur l'équation diophantienne
 . 4/n = 1/x + 1/y + 1/z.
. 4/n = 1/x + 1/y + 1/z. - La conjecture d'Erdős sur les progressions arithmétiques sur les suites dont la somme des inverses diverge.
- La conjecture d'Erdős-Woods sur les nombres déterminés par l'ensemble des diviseurs premiers des k nombres suivants.
- La conjecture d'Erdős-Szekeres sur le nombre de points requis pour qu'un ensemble de points contienne un grand polygone convexe.
- La conjecture d'Erdős-Turán démontrée par Szemerédi
- La conjecture d'Erdős-Turán sur les bases additives d'entiers naturels.
- Une conjecture sur la suite de Sylvester.
- Une conjecture sur les colorations équitables prouvée en 1970 par András Hajnal et Endre Szemerédi, connue maintenant sous le nom théorème de Hajnal-Szemerédi.
- Une conjecture, formulée avec Norman Oler, sur remplissage d'un triangle par des cercles (en) avec un nombre de cercles inférieur, d'une unité, à un nombre triangulaire.
- Le problème des distances distinctes d'Erdős.
Notes et références[modifier | modifier le code]
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Erdős conjecture » (voir la liste des auteurs).
Voir aussi[modifier | modifier le code]
Article connexe[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- [PDF] (en) Fan Chung, Open problems of Paul Erdős in graph theory
- Liste de sujets nommés d'après Paul Erdős (en)
Source : wikipedia
21:02 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Conjecture d'Erdős-Graham
Conjecture d'Erdős-Graham
En théorie combinatoire des nombres, la conjecture d'Erdős-Graham, aujourd'hui résolue, assure que dans toute partition finie de l'ensemble des entiers supérieurs ou égaux à 2, un sous-ensemble de l'une des parties peut servir à représenter 1 par une fraction égyptienne, c'est-à-dire que pour tout r > 0 et toute coloration des entiers 2, 3, 4, … par rcouleurs, il existe un ensemble fini monochrome S tel que

Plus précisément, Paul Erdős et Ronald Graham avaient conjecturé, parmi les nombreux problèmes sur les fractions égyptiennes, l'existence d'une constante b (nécessairement supérieure ou égale à e) telle que pour tout r assez grand, le plus grand élément de S puisse être majoré par br.
Ernest S. Croot III (en) a démontré leur conjecture en 2000 dans sa thèse de Ph.D.1 puis, en post-doc à l'UC Berkeley, a publié sa preuve dans une revue2. La valeur qu'il donne pour b est e167 000. Son résultat est un corollaire d'un théorème où il établit l'existence de représentations de 1 par des fractions égyptiennes pour des ensembles C de nombres lisses dans des intervalles de la forme [X, X1+δ], si C contient assez de nombres pour que la somme de leurs inverses soit au moins égale à 6. La conjecture d'Erdős-Graham s'en déduit en montrant qu'on peut trouver un intervalle de cette forme dans lequel la somme des inverses de tous les nombres lisses vaut au moins 6r ; par conséquent, si les entiers sont colorés par r couleurs, il doit exister une partie C monochrome satisfaisant les conditions de la conjecture.
Notes et références[modifier | modifier le code]
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Erdős–Graham problem » (voir la liste des auteurs).
- (en) Ernest S., III Croot, Unit Fractions : Ph.D. thesis, Athens, Univ. Georgia,
- (en) Ernest S., III Croot, « On a coloring conjecture about unit fractions », Ann. Math., vol. 157, no 2, , p. 545-556, arXiv:math.NT/0311421 [archive]
Article connexe[modifier | modifier le code]
21:01 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Parcours de Graham
Parcours de Graham
Le parcours de Graham est un algorithme déterminant l'enveloppe convexe d'un ensemble de points. Son principal intérêt est sa complexité algorithmique en O(n log n). Cet algorithme doit son nom à Ronald Graham, qui a publié l'algorithme original en 19721.
Sommaire
[masquer]
Algorithme[modifier | modifier le code]
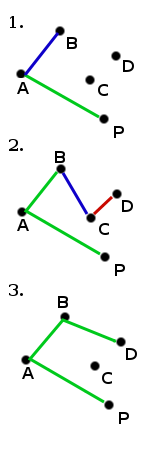
La première étape de cet algorithme consiste à rechercher le point de plus petite ordonnée. S'il y a égalité entre un ou plusieurs points, l'algorithme choisit parmi eux le point de plus petite abscisse. Nommons P ce point. La complexité en temps de cette étape est en O(n), n étant le nombre de points de l'ensemble.
L'ensemble des points (P compris) est ensuite trié en fonction de l'angle que chacun d'entre eux fait avec l'axe des abscisses relativement à P. N'importe quel algorithme de tri convient pour cela, par exemple le tri par tas (qui a une complexité de O(n log n)). Pour cela, il n'est pas nécessaire de calculer l'angle réel ; on peut se limiter à la comparaison des tangentes, ou bien même utiliser le produit en croix des coordonnées pour connaître les positions relatives des points. À l'issue de cette étape, on dispose d'un tableau T contenant les points ainsi triés.
L'algorithme considère ensuite successivement les séquences de trois points contigus dans le tableau T, vus comme deux couples successifs. Pour chacune de ces paires de couples, il décide si passer du premier couple au second constitue un « tournant à gauche » ou un « tournant à droite ». Si c'est un « tournant à droite », cela signifie que l'avant dernier point considéré (le deuxième des trois) ne fait pas partie de l'enveloppe convexe, et qu'il doit être rejeté de T. Cette analyse se répète ensuite, tant que l'ensemble des trois derniers points est un « tournant à droite ». Dès que l'on rencontre un « tournant à gauche », l'algorithme passe au point suivant de T. (Si l'on rencontre trois points alignés, à quelque étape que ce soit, on peut choisir de conserver ou de rejeter le point considéré, au choix, suivant la définition que l'on choisit pour l'enveloppe convexe : en effet certaines applications requièrent que tous les points sur l'enveloppe soient compris dans l'enveloppe.)
Ici encore, déterminer si trois points constituent un « tournant à gauche » ou un « tournant à droite » ne requiert pas de calculer l'angle réel entre les deux segments, et peut être réalisé par simple arithmétique. Pour trois points (x1, y1), (x2, y2) et (x3, y3), il suffit de calculer le sens du produit vectoriel des deux vecteurs définis par les points (x1, y1), (x2, y2) et (x1, y1), (x3, y3), donné par le signe de l'expression (x2-x1)(y3-y1)-(y2-y1)(x3-x1). Si le résultat est nul, les points sont alignés. S'il est positif, les trois points constituent un « tournant à gauche », dans le cas contraire c'est un « tournant à droite ».
Ce processus retournera finalement au point auquel il a commencé, auquel cas l'algorithme sera terminé, et T contiendra alors les points formant l'enveloppe convexe, dans l'ordre inverse des aiguilles d'une montre.
Complexité algorithmique[modifier | modifier le code]
Le tri des points peut se faire avec une complexité en temps en O(n log n). La complexité de la boucle principale peut sembler être O(n2), parce que l'algorithme revient en arrière à chaque point pour évaluer si l'un des points précédents est un « tournant à droite ». Mais elle est en fait en O(n), parce que chaque point n'est considéré qu'une seule fois. Ainsi, chaque point analysé ou bien termine la sous-boucle, ou bien est retiré de T et n'est donc plus jamais considéré. La complexité globale de l'algorithme est donc en O(n log n), puisque la complexité du tri domine la complexité du calcul effectif de l'enveloppe convexe.
Pseudo-code[modifier | modifier le code]
Soit Points l'ensemble de points à examiner, sous la forme d'un tableau indexé à partir de un, et Pile une pile qui contiendra le résultat final.
Trouver le pivot P;
Trier les points par angle (les points d'angle égal seront triés par rapport à leur abscisse);
# Points[1] est le pivot, Points[longueur] aussi (fin du circuit)
Pile.empiler(Points[1]);
Pile.empiler(Points[2]);
POUR i = 3 A Points.longueur
TANT QUE (Pile.hauteur >= 2) ET (Produit_vectoriel(Pile.second, Pile.haut, Points[i]) ≤ 0)
Pile.dépiler;
FIN TANT QUE
Pile.empiler(Points[i]);
FIN POUR
FONCTION Produit_vectoriel(p1, p2, p3)
RENVOYER(p2.x - p1.x)*(p3.y - p1.y) - (p3.x - p1.x)*(p2.y - p1.y);
FIN FONCTION
Explication du pseudo code:
Pile.haut : renvoie le sommet tout en haut de la pile S
Pile.second : renvoie le sommet juste avant Pile.haut
Produit_vectoriel(p1,p2,p3)≤0 : p3 est à droite du segment [p1,p2]
Note: pour gérer les cas dégénérés où l'enveloppe convexe a moins de trois points, un seul point devrait être entré dans la pile au départ, et si jamais la pile a moins de deux points (elle en aura au moins toujours un), alors le haut de la pile devrait être également sorti si le nouveau point est le point considéré. En d'autres termes, la condition du « tant que » devrait être comme suit.
Pile.hauteur >= 2 ? Produit_vectoriel(Pile.second, Pile.haut, Points[i])≤ 0 : Pile.haut == Points[i]
Notes et références[modifier | modifier le code]
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Graham scan » (voir la liste des auteurs).
- (en) R. L. Graham, An Efficient Algorithm for Determining the Convex Hull of a Finite Planar Set' [archive], Information Processing Letters 1, 1972, p. 132-133.
Voir aussi[modifier | modifier le code]
Article connexe[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- (en) Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein, Introduction to Algorithms, MIT Press et McGraw-Hill, , 2e éd. [détail de l’édition](ISBN 0-262-03293-7, 978-0-262-03293-3 et 978-0-262-53196-2). Pages 949–955 de la section 33.3: Finding the convex hull.
- (en) Implémentations du parcours de Graham en C++ et en Pascal Objet.
- [PDF] Présentation d'algorithmes pour calculer l'envelopper convexe d'un nuage de points
Source : wikipedia
21:00 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Nombre de Graham
Nombre de Graham
Le nombre de Graham, du nom du mathématicien Ronald Graham, est un entier naturel connu pour avoir été longtemps le plus grand entier apparaissant dans une démonstration mathématique1. Il est beaucoup trop grand pour être écrit grâce à la notation scientifique et nécessite une notation permettant d'écrire de très grands nombres. Toutefois, il est possible d'obtenir ses derniers chiffres sans trop de difficulté (les dix derniers sont …2464195387).
Sommaire
[masquer]
Le problème de Graham[modifier | modifier le code]
Le nombre de Graham entretient un lien avec une branche des mathématiques connue sous le nom de théorie de Ramsey :
Soit un hypercube de dimension n dont on relie tous les couples de sommets pour obtenir un graphe complet à 2n sommets. Si l'on colore chacune des 2n–1(2n– 1) arêtes du graphe en bleu ou en rouge, quelle est la plus petite valeur de n telle que pour chaque façon de colorer le graphe, il existe un sous-graphe complet monochrome sur quatre sommets coplanaires ?
On ne connait pas encore la réponse à cette question, mais on sait depuis 20032 que ce plus petit n doit être supérieur ou égal à 11 et depuis 20083 qu'il vaut même au moins 13.
Quant aux majorants de ce plus petit n, le meilleur connu en 1971 était4

(il a été affiné depuis5).
Ce nombre est énorme, mais encore moins que le « nombre de Graham » G ci-dessous. Le nombre G doit sa célébrité et son nom à ce qu'il a été présenté en 1977 par Martin Gardner, dans le Scientific American, comme un majorant dû à Graham6, au lieu7 du majorant bien plus précis ci-dessus, trouvé par Graham et Rothschild (en).
Définition[modifier | modifier le code]
Le nombre de Graham est le 64e terme de la suite :

où chaque terme est le nombre de flèches du terme suivant, en utilisant la notation des flèches de Knuth.
De façon équivalente, soit f(n) = hyper(3, n + 2, 3) = 3 → 3 → n ; alors le nombre de Graham est la valeur de la 64e itérée de la fonction f au point 4.
Le nombre de Graham G lui-même ne s'exprime pas commodément avec la notation des flèches chaînées de Conway, mais on a l'encadrement

Notes et références[modifier | modifier le code]
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Graham's number » (voir la liste des auteurs).
- Vers la fin des années 1980, des entiers bien plus grands que le nombre de Graham sont apparus dans plusieurs démonstrations mathématiques sérieuses, par exemple en relation avec les formes finies du théorème de Kruskal découvertes par Harvey Friedman.
- (en) Geoffrey Exoo, « A Euclidean Ramsey Problem », Discrete Comput. Geom., vol. 29, no 2, , p. 223-227 (DOI 10.1007/s00454-002-0780-5).
- (en) Jerome Barkley, « Improved lower bound on an Euclidean Ramsey problem », (arXiv 0811.1055).
- (en) R. L. Graham et B. L. Rothschild, « Ramsey's theorem for n-parameter sets », Trans. Amer. Math. Soc., vol. 159, , p. 257-292 (lire en ligne [archive]) (p. 290).
- (en) Mikhail Lavrov, Mitchell Lee et John Mackey, « Graham's number is less than 2 ↑↑↑ 6 », (arXiv 1304.6910). Commentaires [archive] de David Roberts : « The title of this paper is misleading […] it is the exact solution to this problem that they are calling 'Graham's number' […] In fact the bound given in the title, 2↑↑↑6, is a simplification, and not the smallest bound arrived at in the paper, which is 2↑↑2↑↑2↑↑9 […] In terms of the function F of Graham and Rothschild, the LLM bound is between F(4) and F(5) ».
- (en) M. Gardner, « Mathematical Games », Scientific American, vol. 237, , p. 18-28 (DOI 10.1038/scientificamerican1177-18). Cette inexactitude est reprise dans (en) Eric W. Weisstein, « Graham's Number [archive] », MathWorld.
- Pour plus de détails, voir (en) John Baez, « A while back I told you about Graham's number... » [archive], .
Annexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
(en) John H. Conway et Richard Guy, The Book of Numbers, Springer-Verlag, 1996, p. 61-62 [lire en ligne]
Lien externe[modifier | modifier le code]
(en) Geoffrey Exoo, « A Ramsey Problem on Hypercubes »
20:59 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Ronald Graham
Ronald Lewis Graham, né le à Taft en Californie, est un mathématicien que l’American Mathematical Society a reconnu comme « l'un des principaux architectes du développement rapide des mathématiques discrètes ces dernières années à l'échelle mondiale »1. Il a effectué d'importants travaux sur la théorie de l'ordonnancement, la géométrie algorithmique, la théorie de Ramsey et les suites quasi-aléatoires.
Il occupe le poste d'expert scientifique en chef à l'Institut des technologies de l'information et de la communication deCalifornie, également connu sous le nom de Cal-(IT) 2 (pour California Institute for Telecommunication and Information Technology), tout en étant professeur titulaire de la chaire Irwin et Joan Jacobs du département d'informatique et d'ingénieriede l'université de Californie à San Diego (UCSD).
Sommaire
[masquer]
Carrière[modifier | modifier le code]
Né à Taft en Californie, il a obtenu son doctorat en mathématiques à l'université de Californie à Berkeley en 1962, sous la direction de Derrick Lehmer2.
En 1977, dans un article traitant d'un problème de la théorie de Ramsey, il donnait un grand nombre comme borne supérieure de la solution. Ce nombre, devenu célèbre depuis en tant que nombre le plus grand jamais utilisé dans une démonstration mathématique sérieuse (et inscrit comme tel dans le livre Guinness des records), est désormais connu comme le nombre de Graham.
Graham a popularisé le concept du nombre d'Erdős, qui doit son nom au très prolifique mathématicien hongrois Paul Erdős(1913-1996). Le nombre d'Erdős d'Erdős lui-même est 0 et celui d'un mathématicien M est le plus petit nombre d'Erdős de tous les mathématiciens avec qui M a cosigné un article mathématique, plus un. Le nombre d'Erdős de Graham vaut 1, car celui-ci a corédigé un article avec Erdős, qui était également un de ses bons amis. Erdős logeait souvent chez lui, le laissant s'occuper de ses publications mathématiques, et même de son argent.
Entre 1993 et 1994, Graham fut président de l’American Mathematical Society (AMS). En 1999, il est devenu membre émérite de l’Association for Computing Machinery. En 2003, il a reçu le prix Leroy P. Steele de l'AMS pour l'ensemble de sa carrière. Ce prix lui a été remis le 16 janvier, lors des Joint Mathematics Meetings (rencontres conjointes de mathématiques) tenues àBaltimore, au Maryland. Graham, un mathématicien prolifique — et plus généralement un homme toujours actif —, a reçu bien d'autres prix au fil des années : il fut l'un des lauréats du prestigieux prix Pólya, l'année même où le prix était décerné pour la première fois ; il fut également parmi les premiers à obtenir la médaille Euler. La Mathematical Association of Americalui a également décerné le prix Lester R. Ford, « … institué en 1964 pour récompenser les auteurs d'articles d'excellence publiés dans The American Mathematical Monthly… »3, ainsi que le prix Carl Allendoerfer, institué en 1976 pour les mêmes raisons, mais pour une autre revue, le Mathematics Magazine4.
Vie personnelle[modifier | modifier le code]
Ronald Graham est marié à Fan Chung, professeur titulaire de la chaire Akamai de « mathématiques de l'Internet » à l'université de Californie à San Diego. Il a quatre enfants — trois filles, Che, Laura, Christy, et un fils, Marc — né d'un précédent mariage.
Il fut présenté dans Ripley's Believe It or Not non seulement comme « l'un des plus célèbres mathématiciens du monde », mais aussi comme « un trampoliniste et un jongleur très doué », ancien président de l’International Jugglers' Association (une association internationale de jongleurs).
Publications[modifier | modifier le code]
En 2003, Ronald Graham avait publié environ 300 articles et cinq livres, dont Concrete Mathematics (mathématiques concrètes) avecDonald Knuth.
Notes et références[modifier | modifier le code]
- (en) Les prix Leroy P. Steele de l'AMS pour 2003 [archive] (PDF format)
- (en) Ronald Graham [archive] sur le site du Mathematics Genealogy Project
- (en) Le prix Lester R. Ford de la MAA [archive]
- (en) Le prix Carl B. Allendoerfer de la MAA [archive]
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Ronald Graham » (voir la liste des auteurs).
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Lien externe[modifier | modifier le code]
20:57 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Des nombres grands, TRÈS grands - Micmaths
20:56 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook











































