Lemme de Higman

 

 

Cet article est une ébauche concernant les mathématiques. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

En mathématiques, le lemme de Higman est un résultat de la théorie des ordres qui affirme que, pour un ensemble muni d'un bel ordre, l'ensemble 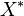des mots finis sur muni de l'ordre sous-mot est également un bel ordre. C'est un cas particulier du théorème de Kruskal sur les arbres, qui se généralise à son tour en le théorème de Robertson-Seymour sur les graphes.

Ce lemme est dû à Graham Higman qui l'a publié en 1952¹.

Notes et références[modifier | modifier le code]

1. ↑ (Higman 1952)

Bibliographie[modifier | modifier le code]

• Graham Higman, « Ordering by divisibility in abstract algebras », Proceedings of the London Mathematical Society, vol. 2, n^o 7,‎ 1952, p. 326-336 (DOI 10.1112/plms/s3-2.1.326)

Lien externe[modifier | modifier le code]

• Notes sur les beaux ordres de Bastien Legloannec.

• Portail des mathématiques

Catégories :

• Théorie des ordres
• Lemme de mathématiques

| [+]