En mathématiques, une algèbre sur un corps commutatif K, ou simplement une K-algèbre, est une structure algébrique (A , + , . , × ) telle que :
- (A, +, ·) est un espace vectoriel sur K,
- la loi × est définie de A x A dans A (loi de composition interne)
- la loi × est distributive par rapport à la loi + .
- pour tout (a, b) dans K2 et pour tout (x, y) dans A2, (a·x)×(b·y) = (ab)·(x×y)
Soient K un corps commutatif et A un espace vectoriel sur K muni de plus d'une opération binaire (c'est-à-dire que le « produit » x×y de deux éléments de A est un élément de A. On dit que A est une algèbre sur K si cette opération binaire est distributive par rapport à + et bilinéaire, ce qui signifie que pour tous vecteurs x, y, z dans A et tous scalaires a, b dans K, les égalités suivantes sont vraies :
On dit que K est le corps de base de A. L'opérateur binaire est souvent désigné comme la multiplication dans A.
Deux algèbres A et B sur K sont isomorphes s'il existe une bijection  telle que
telle que

- Généralisation
Dans la définition, K peut être un anneau commutatif unitaire, et A un K-module. Alors, A est encore appelée une K-algèbre et on dit que K est l'anneau de base de A.
- Algèbres associatives, algèbres commutatives et alèbres unifères
Une algèbre associative est une algèbre sur un anneau dont la loi de composition interne x est associative. Lorsque cet anneau est un corps, il s'agit donc d'une
Une algèbre est dite unifère si elle admet un élément neutre 1 pour la multiplication x. Une algèbre est dite commutative, si la loi de composition interne x est commutative.
Bases et tables de multiplication d'une algèbre sur un corps[modifier]
Tout espace vectoriel admet une base. Une base d'une algèbre A sur un corps K est une base de A pour sa structure d'espace vectoriel1.
Si  est une base de A, il existe alors une unique famille
est une base de A, il existe alors une unique famille  d'éléments du corps K tels que :
d'éléments du corps K tels que :
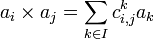
.
Pour i et j fixés, les coefficients sont nuls sauf un nombre fini d'entre eux. On dit que  sont les constantes de structure1 de l'algèbre A par rapport à la base a, et que les relations
sont les constantes de structure1 de l'algèbre A par rapport à la base a, et que les relations  constituent la table de multiplication de l'algèbre A1.
constituent la table de multiplication de l'algèbre A1.
Cette section est vide, insuffisamment détaillée ou incomplète.
Votre aide est la bienvenue !
Exemples d'algèbres de dimension finie[modifier]
- Algèbres associatives et commutatives
Une base de l'algèbre  est constituée des éléments 1 et i. La table de multiplication est constituée des relations :
est constituée des éléments 1 et i. La table de multiplication est constituée des relations :
- Tout corps fini est une algèbre associative, unifère et commutative de dimension n sur son sous-corps premier (
 ), donc son ordre est pn.
), donc son ordre est pn.
Par exemple le corps fini 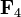 est une algèbre de dimension 2 sur le corps
est une algèbre de dimension 2 sur le corps  dont la table de multiplication dans une base (1, a) est :
dont la table de multiplication dans une base (1, a) est :
- On peut démontrer que toute algèbre unifère de dimension 2 sur un corps est associative et commutative2. Sa table de multiplication dans une base (1, x) est de la forme :
Une telle algèbre est appelée algèbre quadratique de type (a, b) (le type dépendant de la base choisie).
- Algèbres associatives et non commutatives
- L'ensemble des matrices carrées d'ordre
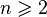 à valeur dans
à valeur dans  ,
,  est une
est une  - algèbre associative, unifère et non commutative de dimension n2.
- algèbre associative, unifère et non commutative de dimension n2.
- L'ensemble des quaternions
 est une
est une  - algèbre associative, unifère et non commutative de dimension 4.
- algèbre associative, unifère et non commutative de dimension 4.
- L'ensemble des biquaternions
 est une
est une  -algèbre associative, unifère et non commutative de dimension 4 qui est isomorphe à l'algèbre
-algèbre associative, unifère et non commutative de dimension 4 qui est isomorphe à l'algèbre  des matrices matrices carrées d'ordre 2 à valeur dans
des matrices matrices carrées d'ordre 2 à valeur dans  .
.
- Algèbre unifère non associative
- L'ensemble des octonions
 est une
est une  - algèbre unifère non associative et non commutative de dimension 8.
- algèbre unifère non associative et non commutative de dimension 8.
- Algèbres non associatives et non unifères
La table de multiplication dans une base orthonormale directe ( ,
,  ,
, 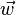 ) est :
) est :
- L'ensemble des matrices carrées d'ordre
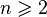 à valeur dans
à valeur dans  , muni du crochet de Lie : [M,N] = MN − NM,
, muni du crochet de Lie : [M,N] = MN − NM, ![left(mathcal M_n(mathbb R), +,cdot, [,] right)](http://upload.wikimedia.org/math/4/9/e/49ebdc968ab715dec75900a90c652c57.png) est une
est une  - algèbre non associative, nonunifère et non commutative de dimension n2. Elle est anti-commutative et possède des propriétés qui font de l'algèbre une algèbre de Lie.
- algèbre non associative, nonunifère et non commutative de dimension n2. Elle est anti-commutative et possède des propriétés qui font de l'algèbre une algèbre de Lie.
- L'ensemble des quaternions
 n'est pas une
n'est pas une  -algèbre car la multiplication
-algèbre car la multiplication  n'est pas
n'est pas  -bilinéaire :
-bilinéaire :  .
.
Notes et références[modifier]
- ↑ a, b et c N. Bourbaki, Algèbre, chapitre III, p. 10.
- ↑ N. Bourbaki, Algèbre, chapitre III, p. 13, proposition 1.
![]() Pour les articles homonymes, voir Algèbre (homonymie).
Pour les articles homonymes, voir Algèbre (homonymie).


 telle que
telle que
 est une base de A, il existe alors une unique famille
est une base de A, il existe alors une unique famille  d'éléments du corps K tels que :
d'éléments du corps K tels que :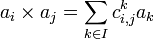 .
.
 sont les constantes de structure1 de l'algèbre A par rapport à la base a, et que les relations
sont les constantes de structure1 de l'algèbre A par rapport à la base a, et que les relations  constituent la table de multiplication de l'algèbre A1.
constituent la table de multiplication de l'algèbre A1. est une
est une  - algèbre associative, unifère et commutative de dimension 2.
- algèbre associative, unifère et commutative de dimension 2. est constituée des éléments 1 et i. La table de multiplication est constituée des relations :
est constituée des éléments 1 et i. La table de multiplication est constituée des relations : ), donc son ordre est pn.
), donc son ordre est pn.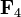 est une algèbre de dimension 2 sur le corps
est une algèbre de dimension 2 sur le corps  dont la table de multiplication dans une base (1, a) est :
dont la table de multiplication dans une base (1, a) est :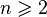 à valeur dans
à valeur dans  ,
,  est une
est une  - algèbre associative, unifère et non commutative de dimension n2.
- algèbre associative, unifère et non commutative de dimension n2. est une
est une  - algèbre associative, unifère et non commutative de dimension 4.
- algèbre associative, unifère et non commutative de dimension 4. est une
est une  -algèbre associative, unifère et non commutative de dimension 4 qui est isomorphe à l'algèbre
-algèbre associative, unifère et non commutative de dimension 4 qui est isomorphe à l'algèbre  des matrices matrices carrées d'ordre 2 à valeur dans
des matrices matrices carrées d'ordre 2 à valeur dans  .
. est une
est une  - algèbre unifère non associative et non commutative de dimension 8.
- algèbre unifère non associative et non commutative de dimension 8. muni du produit vectoriel
muni du produit vectoriel  est une
est une  - algèbre non associative, non unifère et non commutative (elle est anti-commutative) de dimension 3.
- algèbre non associative, non unifère et non commutative (elle est anti-commutative) de dimension 3. ,
,  ,
, 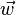 ) est :
) est :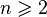 à valeur dans
à valeur dans  , muni du crochet de Lie : [M,N] = MN − NM,
, muni du crochet de Lie : [M,N] = MN − NM, ![left(mathcal M_n(mathbb R), +,cdot, [,] right)](http://upload.wikimedia.org/math/4/9/e/49ebdc968ab715dec75900a90c652c57.png) est une
est une  - algèbre non associative, nonunifère et non commutative de dimension n2. Elle est anti-commutative et possède des propriétés qui font de l'algèbre une algèbre de Lie.
- algèbre non associative, nonunifère et non commutative de dimension n2. Elle est anti-commutative et possède des propriétés qui font de l'algèbre une algèbre de Lie. n'est pas une
n'est pas une  -algèbre car la multiplication
-algèbre car la multiplication  n'est pas
n'est pas  -bilinéaire :
-bilinéaire :  .
. ,
, ,
, ,
,
 ,
,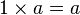 ,
, ,
,
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook









































Les commentaires sont fermés.