08/03/2011
Table of mathematical symbols
This is a listing of common symbols found within all branches of mathematics. Each symbol is listed in both HTML, which depends on appropriate fonts to be installed, and in TEX, as an image. In mathematics written in Arabic, some symbols may be reversed to make right-to-left reading easier. [11] Some Unicode charts of mathematical operators: Some Unicode cross-references:Table of mathematical symbols
Common symbols
See also
Variations
References
External links
Contents[hide] |
| Symbol in HTML | Symbol in TEX | Name | Explanation | Examples |
|---|---|---|---|---|
| Read as | ||||
| Category | ||||
 |
is equal to; equals
everywhere
|
x = y means x and y represent the same thing or value. | 2 = 2 1 + 1 = 2 |
|
 |
is not equal to; does not equal
everywhere
|
x ≠ y means that x and y do not represent the same thing or value. (The forms !=, /= or <> are generally used in programming languages where ease of typing and use of ASCII text is preferred.) |
2 + 2 ≠ 5 | |
  |
is less than, is greater than
|
x < y means x is less than y. x > y means x is greater than y. |
3 < 4 5 > 4 |
|
|
is a proper subgroup of
|
H < G means H is a proper subgroup of G. | 5Z < Z A3 < S3 |
||
  |
(very) strict inequality
is much less than, is much greater than
|
x ≪ y means x is much less than y. x ≫ y means x is much greater than y. |
0.003 ≪ 1000000 | |
|
asymptotic comparison
is of smaller order than, is of greater order than
|
f ≪ g means the growth of f is asymptotically bounded by g. (This is I. M. Vinogradov's notation. Another notation is the Big O notation, which looks like f = O(g).) |
x ≪ ex | ||
  |
is less than or equal to, is greater than or equal to
|
x ≤ y means x is less than or equal to y. x ≥ y means x is greater than or equal to y. (The forms <= and >= are generally used in programming languages where ease of typing and use of ASCII text is preferred.) |
3 ≤ 4 and 5 ≤ 5 5 ≥ 4 and 5 ≥ 5 |
|
|
is a subgroup of
|
H ≤ G means H is a subgroup of G. | Z ≤ Z A3 ≤ S3 |
||
|
is reducible to
|
A ≤ B means the problem A can be reduced to the problem B. Subscripts can be added to the ≤ to indicate what kind of reduction. | If then |
||
|
≺
|
 |
is Karp reducible to; is polynomial-time many-one reducible to
|
L1 ≺ L2 means that the problem L1 is Karp reducible to L2.[1] | If L1 ≺ L2 and L2 ∈ P, then L1 ∈ P. |
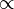 |
is proportional to; varies as
everywhere
|
y ∝ x means that y = kx for some constant k. | if y = 2x, then y ∝ x. | |
|
is Karp reducible to; is polynomial-time many-one reducible to
|
A ∝ B means the problem A can be polynomially reduced to the problem B. | If L1 ∝ L2 and L2 ∈ P, then L1 ∈ P. | ||
 |
plus; add
|
4 + 6 means the sum of 4 and 6. | 2 + 7 = 9 | |
|
the disjoint union of ... and ...
|
A1 + A2 means the disjoint union of sets A1 and A2. | A1 = {3, 4, 5, 6} ∧ A2 = {7, 8, 9, 10} ⇒ A1 + A2 = {(3,1), (4,1), (5,1), (6,1), (7,2), (8,2), (9,2), (10,2)} |
||
 |
minus; take; subtract
|
9 − 4 means the subtraction of 4 from 9. | 8 − 3 = 5 | |
|
negative; minus; the opposite of
|
−3 means the negative of the number 3. | −(−5) = 5 | ||
|
minus; without
|
A − B means the set that contains all the elements of A that are not in B. (∖ can also be used for set-theoretic complement as described below.) |
{1,2,4} − {1,3,4} = {2} | ||
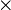 |
times; multiplied by
|
3 × 4 means the multiplication of 3 by 4. (The symbol * is generally used in programming languages, where ease of typing and use of ASCII text is preferred.) |
7 × 8 = 56 | |
|
the Cartesian product of ... and ...; the direct product of ... and ...
|
X×Y means the set of all ordered pairs with the first element of each pair selected from X and the second element selected from Y. | {1,2} × {3,4} = {(1,3),(1,4),(2,3),(2,4)} | ||
|
cross
|
u × v means the cross product of vectors u and v | (1,2,5) × (3,4,−1) = (−22, 16, − 2) |
||
|
the group of units of
|
R× consists of the set of units of the ring R, along with the operation of multiplication. This may also be written R* as described below, or U(R). |
![begin{align} (mathbb{Z} / 5mathbb{Z})^times & = { [1], [2], [3], [4] } \ & cong C_4 \ end{align}](http://upload.wikimedia.org/math/0/6/f/06f5c6ec9c5a7c6e00e8fd5e18529e9e.png) |
||
 |
times; multiplied by
|
3 · 4 means the multiplication of 3 by 4. | 7 · 8 = 56 | |
|
dot
|
u · v means the dot product of vectors u and v | (1,2,5) · (3,4,−1) = 6 | ||
  |
divided by; over
|
6 ÷ 3 or 6 ⁄ 3 means the division of 6 by 3. | 2 ÷ 4 = .5 12 ⁄ 4 = 3 |
|
|
mod
|
G / H means the quotient of group G modulo its subgroup H. | {0, a, 2a, b, b+a, b+2a} / {0, b} = {{0, b}, {a, b+a}, {2a, b+2a}} | ||
|
quotient set
mod
|
A/~ means the set of all ~ equivalence classes in A. | If we define ~ by x ~ y ⇔ x − y ∈ ℤ, then ℝ/~ = {x + n : n ∈ ℤ : x ∈ (0,1]} |
||
 |
plus or minus
|
6 ± 3 means both 6 + 3 and 6 − 3. | The equation x = 5 ± √4, has two solutions, x = 7 and x = 3. | |
|
plus or minus
|
10 ± 2 or equivalently 10 ± 20% means the range from 10 − 2 to 10 + 2. | If a = 100 ± 1 mm, then a ≥ 99 mm and a ≤ 101 mm. | ||
 |
minus or plus
|
6 ± (3 ∓ 5) means both 6 + (3 − 5) and 6 − (3 + 5). | cos(x ± y) = cos(x) cos(y) ∓ sin(x) sin(y). | |
 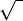 |
the (principal) square root of
|
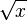 means the nonnegative number whose square is x. means the nonnegative number whose square is x. |
 |
|
|
the (complex) square root of
|
if  is represented in polar coordinates with is represented in polar coordinates with  , then , then 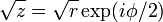 . . |
 |
||
|
|…|
|
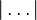 |
absolute value or modulus
absolute value of; modulus of
|
|x| means the distance along the real line (or across the complex plane) between x and zero. | |3| = 3 |–5| = |5| = 5 | i | = 1 | 3 + 4i | = 5 |
|
Euclidean norm or Euclidean length or magnitude
Euclidean norm of
|
|x| means the (Euclidean) length of vector x. | For x = (3,-4)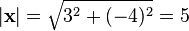 |
||
|
determinant of
|
|A| means the determinant of the matrix A |  |
||
|
cardinality of; size of; order of
|
|X| means the cardinality of the set X. (# may be used instead as described below.) |
|{3, 5, 7, 9}| = 4. | ||
|
||…||
|
 |
norm of; length of
|
|| x || means the norm of the element x of a normed vector space.[3] | || x + y || ≤ || x || + || y || |
|
nearest integer to
|
||x|| means the nearest integer to x. (This may also be written [x], ⌊x⌉, nint(x) or Round(x).) |
||1|| = 1, ||1.6|| = 2, ||−2.4|| = −2, ||3.49|| = 3 | ||
  |
divides
|
a|b means a divides b. a∤b means a does not divide b. (This symbol can be difficult to type, and its negation is rare, so a regular but slightly shorter vertical bar | character can be used.) |
Since 15 = 3×5, it is true that 3|15 and 5|15. | |
|
given
|
P(A|B) means the probability of the event a occurring given that boccurs. | if X is a uniformly random day of the year P(X is May 25 | X is in May) = 1/31 | ||
|
restriction of … to …; restricted to
|
f|A means the function f restricted to the set A, that is, it is the function with domain A ∩ dom(f) that agrees with f. | The function f : R → R defined by f(x) = x2 is not injective, but f|R+is injective. | ||
|
such that
such that; so that
everywhere
|
| means “such that”, see ":" (described below). | S = {(x,y) | 0 < y < f(x)} The set of (x,y) such that y is greater than 0 and less than f(x). |
||
|
||
|
 |
is parallel to
|
x || y means x is parallel to y. | If l || m and m ⊥ n then l ⊥ n. |
|
is incomparable to
|
x || y means x is incomparable to y. | {1,2} || {2,3} under set containment. | ||
|
exact divisibility
exactly divides
|
pa || n means pa exactly divides n (i.e. pa divides n but pa+1 does not). | 23 || 360. | ||
 |
cardinality of; size of; order of
|
#X means the cardinality of the set X. (|…| may be used instead as described above.) |
#{4, 6, 8} = 3 | |
|
connected sum of; knot sum of; knot composition of
|
A#B is the connected sum of the manifolds A and B. If A and Bare knots, then this denotes the knot sum, which has a slightly stronger condition. | A#Sm is homeomorphic to A, for any manifold A, and the sphereSm. | ||
 |
aleph
|
ℵα represents an infinite cardinality (specifically, the α-th one, where α is an ordinal). | |ℕ| = ℵ0, which is called aleph-null. | |
 |
beth
|
ℶα represents an infinite cardinality (similar to ℵ, but ℶ does not necessarily index all of the numbers indexed by ℵ. ). |  |
|
|
19:34 | Lien permanent | Commentaires (0) | |

































 del.icio.us
del.icio.us
 Digg
Digg
Les commentaires sont fermés.