19/11/2010
Primalité dans un anneau
En algèbre commutative, dans un anneau intègre, un élément p est dit irréductible s'il n'est ni nul, ni inversible, ni produit de deux éléments non inversibles. Il est dit premier s'il n'est ni nul ni inversible et si, pour tout produit ab divisible par p, l'un des deux facteurs a ou b est divisible par p. Tout élément premier est irréductible. Dans un anneau factoriel (comme l'anneau des entiers ou l'anneau des polynômes à coefficients dans un corps), ces deux notions sont équivalentes. Deux éléments a et b sont dits premiers entre eux si tout diviseur commun à a et b est inversible.Primalité dans un anneau
Sommaire[masquer] |
Dans l'anneau des entiers, il existe différentes caractérisations des nombres premiers et des nombres premiers entre eux qui, dans un anneau quelconque, conduisent à trois couples de notions différentes. Dans la suite, A est un anneau commutatif unifère intègre et a, b, p sont des éléments de A. Un idéal de A est dit propre s'il est différent de A. La notation (a)désigne l'idéal principal engendré par a (c'est-à-dire l'ensemble des multiples de a). Conditions équivalentes : Probablement par influence des polynômes, la notion suivante n'est pas baptisée "élément premier", mais "élément irréductible" : Conditions équivalentes : Conditions équivalentes (d'après les deux dernières, cette notion est donc symétrique en a et b) : La définition correspondante est alors : Conditions équivalentes : La notion d'éléments étrangers correspond à la caractérisation des nombres premiers entre eux par le théorème de Bachet-Bézout. La définition correspondante est alors : Conditions équivalentes : Dans les contre-exemples ci-dessous, K désigne un corps et A le sous-anneau de K[X,Y] formé des polynômes dont chaque monôme est de degré total pair. Serge Lang, Algèbre [détail des éditions]Introduction [modifier]
Éléments premiers entre eux et élément irréductible [modifier]
 n’est inclus dans aucun idéal principal propre de
n’est inclus dans aucun idéal principal propre de  .
.
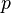 est irréductible s'il n'est ni nul ni inversible et s'il est premier avec tout élément qu'il ne divise pas.
est irréductible s'il n'est ni nul ni inversible et s'il est premier avec tout élément qu'il ne divise pas.
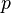 n'est ni nul, ni inversible, ni produit de deux éléments non inversibles
n'est ni nul, ni inversible, ni produit de deux éléments non inversibles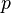 n'est ni nul ni inversible, et ses seuls diviseurs sont les inversibles ou les éléments associés à
n'est ni nul ni inversible, et ses seuls diviseurs sont les inversibles ou les éléments associés à 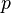
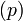 est non nul, et maximal dans l’ensemble des idéaux principaux propres de
est non nul, et maximal dans l’ensemble des idéaux principaux propres de  .
.Éléments indissolubles entre eux et élément premier [modifier]
si a divise bx alors a divise x.
Éléments étrangers et élément extrémal [modifier]
Liens entre ces trois notions [modifier]
Les réciproques sont fausses :
Dans ![K[X,Y]~](http://upload.wikimedia.org/math/f/8/9/f890d50fe1d52623aabfbc6d992e1133.png) ,
,  et
et 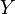 sont indissolubles entre eux mais pas étrangers.
sont indissolubles entre eux mais pas étrangers.
Dans  ,
, 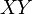 et
et 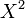 sont premiers entre eux mais pas indissolubles entre eux (car
sont premiers entre eux mais pas indissolubles entre eux (car 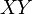 divise
divise 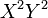 mais pas
mais pas  ).
).
Les réciproques sont fausses :
Dans ![K[X,Y]~](http://upload.wikimedia.org/math/f/8/9/f890d50fe1d52623aabfbc6d992e1133.png) ,
,  est premier non extrémal.
est premier non extrémal.
Dans  ,
, 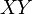 est irréductible mais non premier (il divise
est irréductible mais non premier (il divise 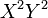 mais ni
mais ni 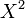 , ni
, ni  ).
).
 ou
ou ![K[X]~](http://upload.wikimedia.org/math/3/e/4/3e4b52cade316b4e28c27bd05f54721f.png) ), les trois notions (étrangers, indissolubles entre eux, premiers entre eux) sont équivalentes (donc irréductible équivaut à premier équivaut à extrémal).
), les trois notions (étrangers, indissolubles entre eux, premiers entre eux) sont équivalentes (donc irréductible équivaut à premier équivaut à extrémal).Bibliographie [modifier]
19:15 Publié dans Primalité dans un anneau | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook








































Les commentaires sont fermés.