Mordell Curve

Mordell Curve

An elliptic curve of the form 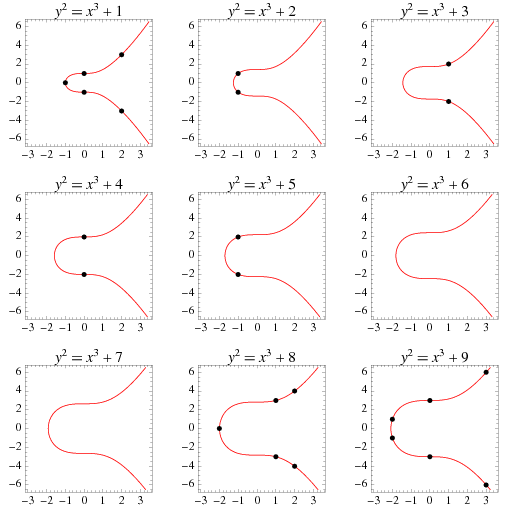 for  an integer. This equation has a finite number of solutions in integers for all nonzero . If  is a solution, it therefore follows that  is as well.

Uspensky and Heaslet (1939) give elementary solutions for , , and 2, and then give , , , and 1 as exercises. Euler found that the only integer solutions to the particular case  (a special case of Catalan's conjecture) are , , and . This can be proved using Skolem's method, using the Thue equation , using 2-descent to show that the elliptic curve has rank 0, and so on. It is given as exercise 6b in Uspensky and Heaslet (1939, p. 413), and proofs published by Wakulicz (1957), Mordell (1969, p. 126), Sierpiński and Schinzel (1988, pp. 75-80), and Metsaenkylae (2003).

Solutions of the Mordell curve with  are summarized in the table below for small .

	solutions
1	(, 0), (0, 1), (2, 3)
2	(, 1)
3	(1, 2)
4	(0, 2)
5	(, 2)
6	none
7	none
8	(, 0), (1, 3), (2, 4), (46, 312)
9	(, 1), (0, 3), (3, 6), (6, 15), (40, 253)
10	(, 3)

Values of  such that the Mordell curve has no integer solutions are given by 6, 7, 11, 13, 14, 20, 21, 23, 29, 32, 34, 39, 42, ... (Sloane's A054504; Apostol 1976, p. 192).

SEE ALSO: Catalan's Conjecture, Catalan's Diophantine Problem, Elliptic Curve

REFERENCES:

Apostol, T. M. Introduction to Analytic Number Theory. New York: Springer-Verlag, 1976.

Cohen, H. "." 24 Nov 2003. http://listserv.nodak.edu/scripts/wa.exe?A2=ind0311&L....

Conrad, M. Untitled. http://emmy.math.uni-sb.de/~simath/MORDELL/MORDELL+.

Gebel, J. "Data on Mordell's Curve." http://tnt.math.metro-u.ac.jp/simath/MORDELL/.

Gebel, J.; Pethő, A.; and Zimmer, H. G. "On Mordell's Equation." Compos. Math. 110, 335-367, 1998.

Llorente, P. and Quer, J. "On the 3-Sylow Subgroup of the Class Group of Quadratic Fields." Math. Comput. 50, 321-333, 1988.

Mestre, J.-F. "Rang de courbes elliptiques d'invariant donné." C.R. Acad. Sci. Paris 314, 919-922, 1992.

Mestre, J.-F. "Rang de courbes elliptiques d'invariant nul." C.R. Acad. Sci. Paris 321, 1235-1236, 1995.

Metsaenkylae, T. "Catalan's Conjecture: Another Old Diophantine Problem Solved." Bull. Amer. Math. Soc. S 0273-0979(03)00993-5, September 5, 2003.

Mordell, L. J. Diophantine Equations. London: Academic Press, 1969.

Myerson, G. "Re: ." 24 Nov 2003. http://listserv.nodak.edu/scripts/wa.exe?A2=ind0311&L....

Quer, J. "Corps quadratiques de 3-rang 6 et courbes elliptiques de rang 12." C.R. Acad. Sci. Paris. Sér. 1 Math. 305, 215-218, 1987.

Sierpiński, W. and Schinzel, A. Elementary Theory of Numbers, 2nd Eng. ed. Amsterdam, Netherlands: North-Holland, 1988.

Sloane, N. J. A. Sequence A054504 in "The On-Line Encyclopedia of Integer Sequences."

Szymiczek, K. "Re: ." 26 Nov 2003. http://listserv.nodak.edu/scripts/wa.exe?A2=ind0311&L....

Uspensky, J. V. and Heaslet, M. A. Elementary Number Theory. New York: McGraw-Hill, 1939.

Wakulicz, A. "On the Equation ." Colloq. Math. 5, 11-15, 1957.

Womack, T. "Minimal-Known Positive and Negative  for Mordell Curves of Given Rank." http://www.maths.nott.ac.uk/personal/pmxtow/mordellc.htm.

CITE THIS AS:

Weisstein, Eric W. "Mordell Curve." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/MordellCurve.html

Contact the MathWorld Team
© 1999-2010 Wolfram Research, Inc. | Terms of Use

Source : http://mathworld.wolfram.com/MordellCurve.html