19/11/2010
Anneau quotient
En mathématiques, un anneau quotient est l'ensemble quotient d'un anneau donné par un de ses idéaux.Anneau quotient
Sommaire[masquer] |
Soient A un anneau et I un idéal bilatère de A. On définit la relation d'équivalence R suivante : Deux éléments de A sont ainsi en relation si leur différence appartient à l'idéal I, c’est-à-dire si ces deux éléments sont congrus modulo I. L'ensemble quotient A/R, que l'on note alors A/I, muni des opérations induites est un anneau, nommé anneau quotient de A par I. L'application p : A → A/I définie par p(x) = x + I est un homomorphisme surjectif d'anneau dont le noyau est l'idéal I. Soit A un anneau commutatif : Les anneaux quotients sont utilisés dans de nombreuses branches des mathématiques. Les exemples sont fréquents en théorie algébrique des nombres, par exemple pour résoudre deséquations diophantiennes. C'est-à-dire des équations à coefficients dans l'anneau Z des entiers naturels dont les solutions recherchées sont entières. L'identité de Bézout peut être vue comme une équation diophantienne de degré un, c'est-à-dire qu'elle correspond à un polynôme de degré un. Elle peut prendre la forme suivante : Une solution peut être vue comme l'inverse de a dans l'anneau quotient Z / b Z. Ainsi, il existe des solutions si et seulement si la classe de a est un élément inversible de l'anneau quotient, i. e. si et seulement si a premier avec b. Les valeurs possibles de x sont éléments de l'inverse de la classe de a. Les équations diophantiennes polynomiales d'ordre deux utilisent aussi la structure d'anneau quotient. Un exemple est un cas particulier de l'équation de Pell-Fermat : Ici, n désigne un entier sans facteur carré. La méthode chakravala correspond à un algorithme simple de détermination d'une solution. Pour montrer sa convergence, on utilise l'anneau des nombres de la forme a + b√n où a et b désignent des entiers. Le fait de montrer que tous les anneaux quotients sont de cardinal fini est une étape clé de la démonstration. Cette équation est analogue à la suivante : Ici n est toujours un entier sans facteur carré et p désigne un nombre premier. L'usage d'un bon anneau A d'entiers quadratiques, c'est-à-dire de nombres de la forme a + b.i.√n où idésigne l'imaginaire pur et l'étude des anneaux quotients de la forme A/J où J est un idéal maximal permet de résoudre l'équation. Des exemples sont donnés dans l'article Entier quadratique. La théorie de Galois fait aussi un large usage des anneaux quotients. Soient K un corps commutatif et K[X] l'anneau des polynômes à coefficients dans K. Un des nombreux objectifs de la théorie est l'étude de l'équation polynomiale P(X) = 0. Si P est un polynôme irréductible, on recherche des solutions dans une extension algébrique L de K. Un cas particulier largement utilisé est K[X]/(P), l'anneau des polynômes quotienté par l'idéal engendré par P(X). Comme P(X) est irréductible, l'idéal engendré par P(X) est maximal, l'anneau quotient est bien un corps. Cette technique permet de construire tous les corps finis. Soit L un corps fini, il existe toujours p un nombre premier et n un entier positif tel que le cardinal de L soit égal à pn. La valeurp correspond à la caractéristique de K.Définition [modifier]
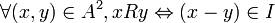

Exemples [modifier]
Propriétés [modifier]
 défini par
défini par  .
.Utilisations [modifier]
Théorie algébrique des nombres [modifier]



Théorie de Galois [modifier]
19:12 Publié dans Anneau quotient | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook








































Les commentaires sont fermés.