03/12/2010
CM2 : Additions et soustractions de nombres décimaux
Exemple : 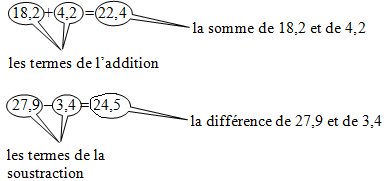
II. Calculer une somme, une différence
a) Poser une addition, une soustraction
Exemple : 
b) A l'aide d'une calculatrice
Exemple : A l'aide d'une calculatrice, calculer : 137,9 + 23,5
On tape : 137.9 + 23.5 =
La calculatrice affiche 161.4
On écrit : 137,9 + 23,5 = 161,4
III. Propriétés
Exemple :
7 + 72 + 3 + 28
= (72 + 28) + (7 + 3)
= 100 + 10
= 110
Remarque :
Regrouper les termes permet d'obtenir des opérations plus faciles à calculer.  Dans une soustraction, l'ordre des termes a de l'importance et on ne peut pas regrouper des termes.
Dans une soustraction, l'ordre des termes a de l'importance et on ne peut pas regrouper des termes.
Exemples :
| 100 - 40 - 15 | 100 - (40 - 15) |
| = 60 - 15 | = 100 - 25 |
| = 45 | = 75 |
IV. Ordre de grandeur d'une somme, d'une différence
Exemple :
Donnons un ordre de grandeur de la somme 2 037,82 + 4 984,75 :
2 037,82 est proche de 2 000.
4 984,75 est proche de 5 000.
Donc un ordre de grandeur de 2 037,82 + 4 984,75 est 2 000 + 5 000, c'est-à-dire 7 000.
Donc : 2 037,82 + 4 984,75 est proche de 7 000.
Exemple :
Donnons un ordre de grandeur de la différence 4 987,87 - 1 824,59 :
4 987,87 est proche de 5 000.
1 824,59 est proche de 2 000.
Donc un ordre de grandeur de 4 987,87 - 1 824,59 est 5 000 - 2 000, soit 3 000.
Donc 4 987,87 - 1 824,59 est proche de 3 000.
Remarque :
Un ordre de grandeur peut servir à prévoir ou à vérifier un résultat.
Exemple :
On a vu qu'un ordre de grandeur de 4 987,87 - 1 824,59 est 3 000.
En posant la soustraction, on trouve : 4 987,87 - 1 824,59 = 3 163,28.
3 163,28 est un nombre proche de 3 000. Le résultat est cohérent.
V. Lien entre addition et soustraction
La différence entre deux nombres est le nombre qu'il faut ajouter à l'un pour obtenir l'autre.
Exemple :
La différence 7 - 2 est le nombre qu'il faut ajouter à 2 pour obtenir 7.
7 - 2 = 5 signifie que 2 + 5 = 7
A une addition, on peut faire correspondre deux soustractions : 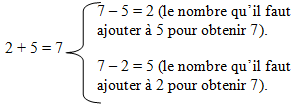
A une soustraction, on peut faire correspondre une addition et une soustraction :
VI. Calcul avec les durées
On utilise la base sexagésimale (de base soixante) pour mesurer le temps :  Dans une heure, il y a 60 minutes : 1 h = 60 min
Dans une heure, il y a 60 minutes : 1 h = 60 min  Dans une minute, il y a 60 secondes : 1 min = 60 s
Dans une minute, il y a 60 secondes : 1 min = 60 s
Exemple 1 :
Combien de temps dure une séance de cinéma qui commence à 15 h 25 et qui finit à 18 h 05 ?
Méthode 1 : On pose la soustraction : 
Méthode 2 :
De 15 h 25 à 16 h s'écoulent 35 min.
De 16 h à 18 h 05 sécoulent 2 h 05 min.35 min + 2 h 05 min = 2 h 40 min
Méthode 3 :
De 15 h 25 à 18 h 25 s'écoulent 3 h.
La séance finit à 18 h 05, soit 20 min avant 18 h 25.
3 h - 20 min = 2 h 40 min.
La séance dure donc 2 h 40 min.
Exemple 2 :
A quelle heure notre train doit-il arriver s'il est parti à 11 h 50 et que la durée du voyage est 4 heures et 20 minutes ? 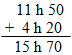
Or, 70 min = 1 h 10 min, donc :
15 h 00 + 70 min = 15 h 00 + 1 h 10 min = 16 h 10 min
Notre train va donc arriver à 16 h 10.
Source : http://www.le-precepteur.net/cm2/mathematiques/additions/...
22:07 Publié dans Additions et soustractions de nombres décimaux | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook







































