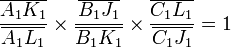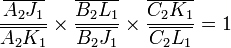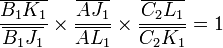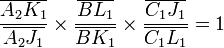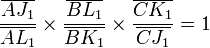theoreme-de-pappus : Mathématique

D	L	M	M	J	V	S
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30

08/12/2010

Théorème de Pappus

Sommaire

Introduction [modifier]

Le théorème de Pappus est un résultat de géométrie présentant deux particularités :

D'abord, parmi tous les théorèmes de géométrie, c'est celui qui demande les hypothèses minimales. Il porte sur deux triplets de points arbitraires respectivement pris sur deux droites coplanaires quelconques. Il ne demande donc comme connaissance que celle de l'alignement de trois points et ne nécessite par exemple ni métrique, ni orthogonalité… On dit qu'il est un théorème de géométrie projective.

Ensuite, ce théorème est le générateur de tous les théorèmes de géométrie euclidienne par l'enchaînement suivant

D'après un résultat obtenu par D. Hilbert, le théorème de Pappus permet de démontrer le théorème des triangles homologiques.

Dans Leçons de géométrie projective du célèbre géomètre F. Enriqués, on lit : …en se servant du théorème des triangles homologiques […] on pourrait déduire tous les théorèmes de géométrie projective plane. (voir page 46 de son livre)

Enfin la géométrie projective contient la géométrie euclidienne comme cas particulier.

On trouvera tous les détails sur ces développements dans les références données en fin d'article. Cette particularité remarquable explique que certains auteurs aient conféré le statut d'axiome à ce théorème, voir axiomes de plans projectifs.

Énoncé du théorème [modifier]

Théorème de Pappus

Dans un plan, soient $A 1$ , $B 1$ , $C 1$ trois points distincts alignés sur une droite $(d)$ , et soient $A 2$ , $B 2$ , $C 2$ trois autres points distincts alignés sur une autre droite 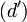$(d^prime)$ alors les points

$A$ intersection de $(B 2 C 1)$ avec $(C 2 B 1)$
$B$ intersection de $(A 2 C 1)$ avec $(C 2 A 1)$
$C$ intersection de $(A 2 B 1)$ avec $(B 2 A 1)$

sont alignés.

Il s'agit d'un théorème de géométrie projective donc les points considérés peuvent être propres ou impropres. Dans le cas où tous les points sont propres, on obtient une configuration du type ci-contre.

Remarques :

si l'on note $(Δ)$ la droite portant les points A,B,C alors les assertions suivantes sont équivalentes (en géométrie projective) :

-- les trois droites $(d)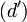$ , $(d^prime)$ et $(Δ)$ sont concourantes ;

-- les trois droites $(A 1 A 2)$ $(B 1 B 2)$ $(C 1 C 2)$ sont concourantes ;

-- les six droites « croisillons » $(B 2 C 1)$ $(C 2 B 1)$ $(A 2 C 1)$ $(C 2 A 1)$ $(A 2 B 1)$ $(B 2 A 1)$ sont tangentes à une même conique.

-- Les deux droites $(d)$ et 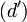$(d^prime)$ peuvent être considérées comme une conique dégénérée : pour l'hexagramme $A 1 B 2 C 1 A 2 B 1 C 2$ , le théorème de Pappus-Pascal affirme l'alignement des points $A$ , $B$ et $C$ .

Démonstration à l'aide des applications projectives [modifier]

Démonstration du théorème

On construit les points O intersection de (d) et (d'), D intersection de $(A 1 B 2)$ et $(A 2 C 1)$ et E intersection de $(A 1 C 2)$ et $(C 1 B 2)$

On considère la projection centrale p de la droite $(A 1 B 2)$ sur la droite (d) de centre $A 2$

$A 1$ a pour image $A 1$
C a pour image $B 1$
D a pour image $C 1$
$B 2$ a pour image O

On considère la projection centrale q de la droite (d) sur la droite $(B 2 C 1)$ de centre $C 2$

$A 1$ a pour image E
$B 1$ a pour image A
$C 1$ pour image $C 1$
O a pour image $B 2$

Par l'application projective q o p de la droite $(A 1 B 2)$ sur la droite $(B 2 C 1)$

$A 1$ a pour image E
C a pour image A
D a pour image $C 1$
$B 2$ a pour image $B 2$

Si on regarde maintenant la projection centrale r de la droite $(A 1 B 2)$ sur la droite $(B 2 C 1)$ de centre B

$A 1$ a pour image E
D a pour image $C 1$
$B 2$ a pour image $B 2$

Or, une application projective d'une droite sur une autre est entièrement déterminée par l'image de trois points distincts. Les transformations q o p et r coïncident sur $A 1$ , D et $B 2$ . Elles sont donc égales et $r (C) = A$ . Les points A, B et C sont donc alignés.

Démonstration à l'aide du théorème de Ménélaüs [modifier]

Démonstration du théorème de Pappus à l'aide de Ménélaüs

Dans le cas où aucun point n'est impropre et à condition qu'il existe un triangle de référence, dont les côtés soient interceptés par cinq droites du problème, on peut caractériser l'alignement de cinq triplets de points grâce au théorème de Ménélaüs et en déduire simplement que les trois points $A$ , $B$ et $C$ sont alignés. Deux triangles de référence peuvent être choisis à cette fin :

le triangle $J 1 K 1 L 1$ (en bleu sur la figure) dont les sommets sont les intersections des droites $(A 2 B 1)$ , $(B 2 C 1)$ et $(A 1 C 2)$ ,
le triangle $J 2 K 2 L 2$ (en rouge sur la figure) dont les sommets sont les intersections des droites $(A 1 B 2)$ , $(B 1 C 2)$ et $(A 2 C 1)$ .

Dans le triangle $J 1 K 1 L 1$ (s'il existe) :

la droite $(A 1 C 1)$ intercepte les trois côtés en $A 1$ , $B 1$ , $C 1$
la droite $(A 2 C 2)$ intercepte les trois côtés en $A 2$ , $B 2$ , $C 2$
la droite $(B 1 C 2)$ intercepte les trois côtés en $B 1$ , $A$ , $C 2$
la droite $(A 2 C 1)$ intercepte les trois côtés en $A 2$ , $B$ , $C 1$
la droite $(A 1 B 2)$ intercepte les trois côtés en $A 1$ , $C$ , $B 2$

D'après Ménélaüs, ces alignements se traduisent par les égalités suivantes :

$frac{overline{A_1K_1}}{overline{A_1L_1}}times frac{overline{B_1J_1}}{overline{B_1K_1}} times frac{overline{C_1L_1}}{overline{C_1J_1}} = 1$

$frac{overline{A_2J_1}}{overline{A_2K_1}}times frac{overline{B_2L_1}}{overline{B_2J_1}} times frac{overline{C_2K_1}}{overline{C_2L_1}} = 1$

$frac{overline{B_1K_1}}{overline{B_1J_1}}times frac{overline{AJ_1}}{overline{AL_1}} times frac{overline{C_2L_1}}{overline{C_2K_1}} = 1$

$frac{overline{A_2K_1}}{overline{A_2J_1}}times frac{overline{BL_1}}{overline{BK_1}} times frac{overline{C_1J_1}}{overline{C_1L_1}} = 1$

$frac{overline{A_1L_1}}{overline{A_1K_1}}times frac{overline{CK_1}}{overline{CJ_1}} times frac{overline{B_2J_1}}{overline{B_2L_1}} = 1$

En multipliant membre à membre ces cinq égalités, il reste après simplification :

$frac{overline{AJ_1}}{overline{AL_1}}times frac{overline{BL_1}}{overline{BK_1}} times frac{overline{CK_1}}{overline{CJ_1}} = 1$

ce qui prouve d'après la réciproque de Ménélaüs l'alignement des trois points $A$ , $B$ et $C$ .

Une démonstration analogue peut être faite dans le triangle $J 2 K 2 L 2$ . Dans ce cas, les trois droites $(B 1 C 2)$ , $(A 2 C 1)$ et $(A 1 B 2)$ (en rouge sur la figure) échangent leur rôle avec les trois droites $(B 2 C 1)$ , $(A 1 C 2)$ et $(A 2 B 1)$ (en bleu sur la figure). Cette fois-ci, les trois premières droites délimitent le triangle de référence tandis que les trois dernières interceptent les côtés du triangle de référence. Les droites $(A 1 C 1)$ et $(A 2 C 2)$ (en vert sur la figure) sont conservées pour intercepter le triangle.

Il existe un moyen pratique de trouver les deux triangles de référence. On peut représenter la ligne brisée $A 1$ , $B 2$ , $C 1$ , $A 2$ , $B 1$ et $C 2$ sous la forme d'un circuit hexagonal. Les côtés opposés de ce circuit hexagonal ont pour intersection les 3 points $A$ , $B$ , $C$ et les deux triangles de référence sont les deux triangles bâtis sur l'hexagone.

Circuit hexagonal et triangles de référence

On peut illustrer sur une autre configuration, avec quelle facilité le circuit hexagonal permet de trouver les deux triangles de référence. Définissons cette fois-ci :

$A$ comme l'intersection de $(A 1 B 2)$ avec $(C 1 C 2)$
$B$ comme l'intersection de $(A 1 A 2)$ avec $(B 1 C 2)$
$C$ comme l'intersection de $(C 1 A 2)$ avec $(B 1 B 2)$

Le circuit hexagonal est alors $A 1$ , $A 2$ , $C 1$ , $C 2$ , $B 1$ et $B 2$ et les deux triangles de référence sont alors :

le triangle $J 1 K 1 L 1$ (en bleu sur la figure) dont les sommets sont les intersections des droites $(A 1 B 2)$ , $(B 1 C 2)$ et $(A 2 C 1)$ ,
le triangle $J 2 K 2 L 2$ (en rouge sur la figure) dont les sommets sont les intersections des droites $(A 2 B 1)$ , $(B 2 C 1)$ et $(A 1 C 2)$ .

Circuit hexagonal et triangles de référence d'une autre configuration

Démonstration du théorème de Pappus à l'aide de Ménélaüs sur une autre configuration

Notions connexes [modifier]

Le Théorème d'Hessenberg qui fait le lien entre le théorème de Pappus et le théorème de Desargues.
Le théorème de Pappus-affine dans le plan affine.
L'Hexagramme de Pascal dont la configuration de Pappus est une version dégénérée (la conique est une bidroite).
Enfin il est indispensable de rappeler que la configuration de Pappus est un bel exemple de Dualité (géométrie projective).

Théorème ou axiome? [modifier]

Tout dépend dans quelle géométrie on se situe. Si on travaille dans un contexte de géométrie euclidienne, cette propriété n'est qu'un théorème découlant d'axiomes plus puissants.

En revanche, dans un contexte de géométrie projective, si on travaille dans un plan projectif pappusien, c'est un de nos axiomes de construction de ce plan. Si on travaille dans un plan projectif homogène, c'est un théorème qui découle d'un autre ensemble d'axiomes.

Sources [modifier]

Leçons de géométrie projective de F. Enriqués
Petite encyclopédie de mathématiques Ed. Didier
Enfin un site où sont donnés de nombreux développements sur le Thèorème de Pappus:Merveilleux Pappus

Articles de géométrie projective ou voisins à consulter.

[modifier]