D	L	M	M	J	V	S
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28

21/11/2010

Théorème d'Abel (analyse)

Source : http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_d'Abel_(a...

Théorème d'Abel (analyse)

Pour les articles homonymes, voir Théorème d'Abel.

Le théorème d'Abel, ou théorème de convergence radiale d'Abel, est un outil central de l'étude des séries entières.

Théorème — Soit $textstyle f(x)= sum_{n geqslant 0} a_n x^n$ une série entière (à coefficients complexes) de rayon de convergence égal à $R$ .

Si 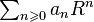$textstylesum_{ngeqslant 0} a_n R^n$ converge, alors :

$lim_{xto R^-} f(x) = sum_{n geqslant 0} a_nR^n$ .

[Dérouler]

Démonstration

Remarque : dans le cas où la série $sum_{n geqslant 0} a_n R^n$ est absolument convergente, le résultat est trivial, il n'y a donc pas lieu d'invoquer ce théorème.

En effet, sous cette condition, $sum_{n geqslant 0} a_n x^n$ converge normalement donc uniformément sur [0, R] ; on retrouve immédiatement :

$lim_{x to R^-} sum_{n=0}^{infty} a_n x^n = sum_{n=0}^{infty} lim_{x to R^-}(a_n x^n) = sum_{n=0}^{infty} a_n R^n$

Exemple (1) :

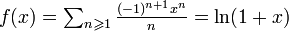Soit $textstyle f(x)= sum_{n geqslant 1} frac{(-1)^{n+1} x^n}{n} = ln (1+x)$ . Comme $textstylesum_{n geqslant 1} frac{(-1)^{n+1}}{n}$ converge (d'après le critère de convergence des séries alternées), on en déduit que : $lim_{x to 1^-} f(x) = ln 2 = sum_{n geqslant 1} frac{(-1)^{n+1}}{n}$

Exemple (2) :

Soit $textstyle g(x)= sum_{n geqslant 0} frac{(-1)^n x^{2n+1}}{2n+1} = arctan (x)$ . Encore par le critère de convergence des séries alternées, on peut affirmer que $textstylesum_{n geqslant 0} frac{(-1)^n}{2n+1}$ converge, d'où : $lim_{x to 1^-} g(x) = arctan (1) = frac{pi}{4} = sum_{n geqslant 0} frac{(-1)^n}{2n+1}$