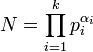suite-aliquote : Mathématique

D	L	M	M	J	V	S
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30

05/12/2010

Suite aliquote

En arithmétique, une suite aliquote est une suite d'entiers dans laquelle chaque nombre est la somme des diviseurs propres¹ de son prédécesseur. Quand la suite atteint 1, elle s'arrête car 1 ne possède pas de diviseur propre.

Ainsi la suite commençant à 10 se comporte de la manière suivante :

u 0 = 10

les diviseurs propres de 10 sont 1, 2 et 5.

u 1 = 1 + 2 + 5 = 8

les diviseurs propres de 8 sont 1, 2 et 4

u 2 = 1 + 2 + 4 = 7

7 ne possède qu'un diviseur propre 1

u 3 = 1

Sommaire

[masquer]

Cas particuliers [modifier]

L'étude des suites aliquotes met en évidence les cas particuliers suivants

si $u 0$ est un nombre premier alors $u 1 = 1$ et la suite s'arrête.
si $u 0$ est un nombre parfait alors la suite est constante
si $u 0$ est un nombre amical, alors $u 1$ est son nombre amical associé et la suite boucle sur ces deux valeurs
si $u 0$ est un nombre sociable alors la suite boucle sur tous les nombres sociables associés à $u 0$

Relation de récurrence [modifier]

La suite est définie par la relation de récurrence suivante : pour tout entier n, si $u n$ est différent de 1

u n + 1 = f (u n)

où f est définie de la manière suivante : si N est un entier différent de 1 dont la décomposition en facteurs premiers est

$N= prod_{i=1}^kp_i^{alpha_i}$

$f(N)=prod_{i=1}^kfrac{p_i^{alpha_i+1}-1}{p_i-1} - N$

On remarque que f est définie par

f (N) = s (N) - N

où s est la fonction diviseur d'ordre 1

Observations et conjectures [modifier]

Toutes les suites aliquotes dont le premier terme est un nombre inférieur ou égal à 100 ont été étudiées et s'arrêtent à 1, sauf les suites constantes commençant par les nombres parfaits 6 et 28. La suite la plus longue est alors obtenue pour un premier terme égal à 30.

Une conjecture importante, due à Catalan, stipule qu'une suite aliquote, ou bien se termine à 1, ou bien finit par être constante sur un nombre parfait, ou périodique sur une famille denombres sociables.

Cette conjecture ne fait pas l'unanimité. En effet, parmi les suites dont le premier terme est un nombre inférieur ou égal à 1000, 5 suites n'ont toujours pas pu être explorées jusqu'à leur terme. Ce sont les suites commençant par 276, 552, 564, 660 et 966. Ces nombres sont appelés les« cinq de Lehmer »². Il existe de même 12 nombres (les douze de Godwin) compris entre 1000 et 2000 pour lesquels les suites aliquotes associées ne sont pas connues.

Il existe des suites aliquotes atteignant des termes astronomiques comme la suite démarrant à 3630 atteignant un nombre à 100 chiffres pour se terminer plus tard à 1³. Hendrick Lenstra a démontré que l'on pouvait toujours trouver une suite aliquote croissante sur n termes consécutifs, quelle que soit la valeur de n.

La quantité $frac{u_{n+1}}{u_n}$ a, elle aussi, été étudiée. La famille des $frac{f(N)}{N}$ n'est pas bornée mais Jean-Luc Garambois conjecture que la moyenne des $frac{f(N)}{N}$ converge vers $(π 2 - 6) / 6$ .

On peut prouver, grâce à la relation de récurrence, que la suite ne change de parité que si l'un des termes s'écrit $a 2$ ou $2 a 2$ .

Bibliographie [modifier]

Jean-Paul Delahaye, Les inattendus mathématiques, Nombres amiables et suites aliquotes

Sites internet [modifier]

www.aliquotes.com

Notes et références [modifier]

↑ Les diviseurs propres de l'entier naturel n non nul, sont les diviseurs positifs de n strictement inférieurs à n
↑ Jean-Paul Delahaye, Les inattendus mathématiques, Nombres amiables et suites aliquotes. (ISBN 2842450736)
↑ (en) Manuel Benito, Wolfgang Creyaufmüller, Juan Varona et Paul Zimmermann , Aliquot sequence 3630 ends after reaching 100 digits [archive]