20/11/2010
Papyrus Rhind
Le papyrus Rhind est un célèbre papyrus de la deuxième période intermédiaire qui aurait été écrit par le scribe Ahmès. Son nom vient de l'Écossais Henry Rhind qui l'acheta en 1858 à Louxor, mais aurait été découvert sur le site de la ville de Thèbes. Au xxie siècle, il est conservé au British Museum ( à Londres). Avec le Papyrus de Moscou, il est une des sources les plus importantes concernant les mathématiques dans l'Égypte antique. Ahmès indique que son papyrus est, en partie, une copie de résultats plus anciens remontant au Moyen Empire (vers -2000). Il contient 87 problèmes résolus d'arithmétique, d'algèbre, de géométrie et d'arpentage, sur plus de 5 m de longueur et 32 cm de large. Il est rédigé enécriture hiératique.Papyrus Rhind
Sommaire[masquer] |
Ces problèmes permettent de comprendre les techniques de multiplication et de division chez les Égyptiens. Voir Mathématiques dans l'Égypte antique#Résolutions d'équations L'arpentage, mesures des distances et les problèmes géométriques qui lui sont liés sont également abordés : aires planes (du trapèze en particulier), volumes de greniers à grains, calcul de pyramides. Les sections R57, R58, R59a et R59b, sont consacrées aux problèmes relatifs à la pente, inclinaison (terme égyptien "skd" avec un point sous le "k") d'une pyramide. Cette inclinaison, qui concerne la ligne de plus grande pente des faces, est exprimée en palmes, unité de longueur qui vaut le septième d'une coudée (voir Mathématiques dans l'Égypte antique). L'examen du contenu de ces sections montre qu'il s'agit, en palmes , de 7 fois la cotangente de l'angle que forme la ligne de plus grande pente avec l'horizontale. Pour le triangle égyptien, elle vaut (3 / 4) x 7 = 21/4 = 5 + 1/4 palmes. Comme ces quatre sections du papyrus, illustrées par un dessin de pyramide, concernent toutes la valeur de 5 + 1/4 palmes, elles attestent qu'il s'agit du triangle égyptien 3, 4, 5 dans ces problèmes de pyramides1. Le papyrus Rhind atteste donc, de façon indirecte par l'inclinaison mais incontestable par la valeur numérique donnée, que la géométrie de la pyramide utilise le triangle égyptien. La pyramide de Khéphren est construite ainsi (voir Mathématiques dans l'Égypte antique). Dans les problèmes 48 et 50, Ahmes étudie le rapport liant l'aire d'un disque à son diamètre en cherchant à ramener l'aire de la circonférence à celle d'un carré équivalent : le papyrus Rhind précise en effet une première approche de la quadrature du cercle (construction d'un carré de même aire qu'un cercle donné) : c'est le carré de côté 8d/9 où d est le diamètre du cercle. En d'autres termes, l'aire d'un cercle de diamètre 9 unités est sensiblement égal à l'aire d'un carré de 8 unités de côté. Cette égalité se traduit par : donc Cette approximation par la quadrature du cercle permit donc aux égyptiens de se passer de la constante π, constante qu'ils connurent seulement à laBasse époque et offrant des résultats moins justes qu'au problème du papyrus Rhind décrit ci-dessus.Algorithmes de multiplication et division (problèmes 1 à 23) [modifier]
Résolution d'équations par la méthode de fausse position (problèmes 24 à 34) [modifier]
Les problèmes d'arpentage (problèmes 41 à 60) [modifier]

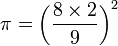 . Ainsi, notre actuel nombre π serait le carré de 16/9, soit : π = 256/81 = 3 + 1/9 + 1/27 + 1/81 = 3,160.
. Ainsi, notre actuel nombre π serait le carré de 16/9, soit : π = 256/81 = 3 + 1/9 + 1/27 + 1/81 = 3,160.Notes [modifier]
Bibliographie [modifier]
Voir aussi [modifier]
Articles connexes [modifier]
Liens externes [modifier]
09:37 Publié dans Papyrus Rhind | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook










































