Source : http://fr.wikipedia.org/wiki/Nombre_superr%C3%A9el

Nombre superréel

Aller à :Navigation,rechercher

En mathématiques, les nombres superréels comprennent une catégorie plus inclusive que les nombres hyperréels.

Supposons que X soit un espace de Tychonoff, aussi appelé un espace 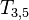, et C(X) une algèbre des fonctions continues à valeurs réelles sur X. Supposons que P soit un idéal premierdans C(X). Alors, l'anneau quotient A = C(X)/P est par définition un domaine intégral qui est une algèbre réelle et qui peut être vue comme totalement ordonnée. Le corps quotient F de A est un corps superréel si F contient strictement les nombres réels , c’est-à-dire que F n'est pas isomorphe à l'ordre de , bien qu'ils peuvent être isomorphes en tant que corps.

Si l'idéal premier P est un idéal maximal, alors F est un corps de nombres hyperréels.

La terminologie est due à Dales et Woodin.

Références [modifier]

• H. Garth Dales and W. Hugh Woodin : Super-Real Fields, Clarendon Press, 1996.

• L. Gillman and M. Jerison : Rings of Continuous Functions, Van Nostrand, 1960.