les-flottants-au-format-double : Mathématique

D	L	M	M	J	V	S
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30

21/01/2010

Les flottants au format double

suivant: Opérations sur les flottants monter: Les réels précédent: Virgule fixe et flottante. Index

Les flottants au format `double`

Cette section développe les notions de la section précédente pour les flottants machine, utilisables dans les langage de programmation usuels, elle peut être omise. La représentation d'un double en mémoire se compose de 3 parties : le bit de signe s = ±1 sur 1 bit, la mantisse M

[0, 2⁵²[ sur 52 bits, et l'exposant e

[0, 2¹¹[ sur 11 bits. Pour les nombres ``normaux'', l'exposant est en fait compris entre 1 et 2¹¹ - 2, le nombre représenté est le rationnel

(1 + $displaystyle {frac{{M}}{{2^{52}}}}$ )2^e+1-2¹⁰

Pour écrire un nombre sous cette forme, il faut d'abord chercher par quel multiple de 2 il faut le diviser pour obtenir un réel r dans [1, 2[, ce qui permet de déterminer l'exposant e. Ensuite on écrit la représentation en base 2 de r - 1

[0, 1[. Exemples :

-2
Signe négatif. Il faut diviser sa valeur absolue 2 par 2¹ pour être entre 1 et 2 dont e + 1 - 2¹⁰ = 1, l'exposant est e = 2¹⁰. On a alors r = 1, r - 1 = 0. Représentation
1 10000000000 00000000...0000
1.5=3/2
Signe positif, compris entre 1 et 2 dont l'exposant vérifie e + 1 - 2¹⁰ = 0 soit e = 2¹⁰ -1 = 2⁹ +2⁸ +2⁷ +2⁶ +2⁵ +2⁴ +2³ +2² +2¹ +2⁰. On a r - 1 = 1/2 = 2^-1. D'où la représentation
0 01111111111 10000000...0000
6.4=32/5
Positif. Il faut le diviser par 2² pour avoir 8/5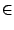 [1, 2[ donc e + 1 - 2¹⁰ = 2 soit e = 2¹⁰ + 1. Ensuite r = 3/5 qu'il faut écrire en base 2 (cf. section précédente), on écrit donc les 52 premiers éléments du développement avec une règle d'arrondi du dernier bit au nombre le plus proche. Ici le bit suivant le dernier 1001 est un 1, on arrondit donc à 1010. D'où la représentation
0 1000000001 100110011001...10011010

On observe que la représentation en base 2 de 6.4 a du être arrondie (car elle est infinie en base 2) bien qu'elle soit exacte (finie) en base 10. Seuls les entiers et les rationnels dont le dénominateur est une puissance de 2 peuvent être représentés exactement. Ceci entraine des résultats qui peuvent surprendre comme par exemple le fait que 0.3 - 3*0.1 n'est pas nul.

Des représentations spéciales (avec e = 0 ou e = 2¹¹ - 1) ont été introduites pour représenter ± (pour les flottants plus grands en valeur absolue que le plus grand flottant représentable), et pour représenter les nombres non nuls plus petits que le plus petit flottant représentable de la manière exposée ci-dessus (on parle de flottants dénormalisés), ainsi que le nombre NaN (Not a Number) lorsqu'une opération a un résultat indéfini (par exemple 0/0).