19/11/2010
Inégalité de Cauchy-Schwarz
En mathématiques, l'inégalité de Cauchy-Schwarz, aussi appelée inégalité de Schwarz1, ou encore inégalité de Cauchy-Bunyakovski-Schwarz2, se rencontre dans de nombreux domaines tels que l'algèbre linéaire, l'analyse avec les séries et en intégration. Cette inégalité s'applique dans le cas d'un espace vectoriel sur le corps des nombres réels ou complexes muni d'un produit scalaire. Dans le cas complexe, le produit scalaire désigne une forme hermitienne définie positive. Son contexte général est donc celui d'un espace préhilbertien. Cette inégalité possède de nombreuses applications, comme le fait d'établir l'inégalité triangulaire montrant que la racine carrée de la forme quadratique associée au produit scalaire est une norme, ou encore que le produit scalaire est continu. Elle fournit des justifications ou des éclairages dans des théories où le contexte préhilbertien n'est pas central. Elle doit son nom à Hermann Amandus Schwarz3 et à Augustin Louis Cauchy4.Inégalité de Cauchy-Schwarz
Sommaire[masquer] |
Le théorème s'énonce couramment de la façon suivante : Théorème 1 — Soit De plus, les deux membres sont égaux si et seulement si x et y sont linéairement dépendants. Les démonstrations présentées ici sont valables aussi bien dans le cadre d'un espace préhilbertien complexe que réel, sauf bien sûr la dernière. Lorsque y=0, l'énoncé est clairement vrai, par conséquent on supposera y non nul. En outre, pour la première démonstration, qui est la plus connue, on suppose que le nombre Posons, pour tout réel t, Par construction, cette expression polynomiale du second degré est positive ou nulle pour tout réel t. On en déduit que son discriminant est négatif ou nul : d'où l'inégalité annoncée. Une variante plus directe est de poser et d'utiliser que (Ce t0 n'est autre que la valeur en laquelle P atteint son minimum, mais cette propriété n'est pas utilisée.) Si (x,y) est lié alors x=λy pour un certain scalaire λ et l'on en déduit immédiatement : Réciproquement, si |<x,y>|=||x|| ||y|| alors le discriminant ci-dessus est nul donc P admet une racine réelle (double) t, et pour ce t on a donc x=-ty, si bien que (x,y) est lié. Ou plus directement (avec le t0 de la variante ci-dessus) : l'hypothèse équivaut à P(t0)=0 donc à x=-t0y. Une variante6 utilise l'identité du théorème de Pythagore. Un calcul direct permet de voir que les vecteurs et donc qui donne l'inégalité souhaitée. Cette démonstration consiste en fait6 à calculer la norme du projeté orthogonal du vecteur x sur la droite vectorielle engendrée par y. L'égalité correspond donc au cas où x et y sont linéairement dépendants. Dans l'espace euclidien (Pour n=3, une preuve et une interprétation géométrique figurent dans identité de Lagrange dans R3). Cette identité se démontre de la façon suivante. L'inégalité de Cauchy-Schwarz a des applications importantes. Elle permet notamment de montrer que l'application Elle permet également de définir l'angle non orienté entre deux vecteurs non nuls d'un espace préhilbertien réel, par la formule : Dans le cas de l'espace euclidien Dans le cas des fonctions à valeurs complexes de carré intégrable7, elle s'écrit Cette inégalité est un cas particulier des inégalités de Hölder. L'inégalité seule est vraie dans le contexte un peu plus général d'un semi-produit scalaire (i.e. sans supposer que la forme quadratique associée est définie), en notant encore || || la semi-norme associée : Théorème 210 — Soit Pour démontrer ce théorème 2, il suffit10 d'ajouter à la preuve algébrique de l'inégalité du théorème 1 un petit argument dans le cas où ||y||=0. Cette inégalité fournit le corollaire suivant. Corollaire10 — Pour qu'une forme bilinéaire symétrique positive (resp. une forme hermitienne positive) soit définie, (il faut et) il suffit qu'elle soit non dégénérée. Le corollaire se démontre de la façon suivante. Pour prouver le sens non immédiat de l'équivalence, supposons que la forme Espace euclidien • Espace hermitien • Forme bilinéaire • Forme quadratique • Forme sesquilinéaire • Orthogonalité • Base orthonormale • Projection orthogonale • Inégalité de Cauchy-Schwarz • Inégalité de Minkowski • Matrice positive • Matrice définie positive • Décomposition QR • Déterminant de Gram •Espace de Hilbert • Base de Hilbert • Théorème spectral • Théorème de Stampacchia • Théorème de Riesz • Théorème de Lax-Milgram • Théorème de représentation de RieszÉnoncé [modifier]
 un espace préhilbertien réel ou complexe. Alors, pour tous vecteurs x et y de E,
un espace préhilbertien réel ou complexe. Alors, pour tous vecteurs x et y de E,
Démonstrations [modifier]
 est réel. On obtient la généralisation du cas étudié par multiplication du vecteur x(ou y) par un nombre complexe convenable de module égal à 1. Ceci étant
est réel. On obtient la généralisation du cas étudié par multiplication du vecteur x(ou y) par un nombre complexe convenable de module égal à 1. Ceci étant  devient réel sans changer de module;
devient réel sans changer de module;  et
et  ne varient pas non plus5.
ne varient pas non plus5.Inégalité [modifier]

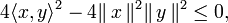
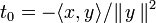
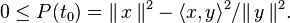
Cas d'égalité [modifier]


Variante géométrique [modifier]
 et
et  sont orthogonaux. Alors, par le théorème de Pythagore on a :
sont orthogonaux. Alors, par le théorème de Pythagore on a :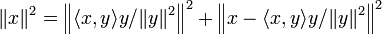 ,
,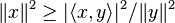
Le cas particulier Rn [modifier]
 muni du produit scalaire usuel
muni du produit scalaire usuel 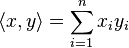 , où
, où 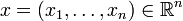 et
et  , une alternative aux démonstrations générales ci-dessus est de déduire l'inégalité (et le cas d'égalité) d'une identité très similaire à celle de la variante géométrique, l'identité de Lagrange, qui s'écrit :
, une alternative aux démonstrations générales ci-dessus est de déduire l'inégalité (et le cas d'égalité) d'une identité très similaire à celle de la variante géométrique, l'identité de Lagrange, qui s'écrit :

Conséquences et applications [modifier]
Conséquences [modifier]
 est une norme car elle vérifie l'inégalité triangulaire. Une conséquence est que le produit scalaire est une fonction continue pour la topologie induite par cette norme.
est une norme car elle vérifie l'inégalité triangulaire. Une conséquence est que le produit scalaire est une fonction continue pour la topologie induite par cette norme.
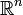 muni du produit scalaire canonique, l'inégalité de Cauchy-Schwarz s'écrit :
muni du produit scalaire canonique, l'inégalité de Cauchy-Schwarz s'écrit :
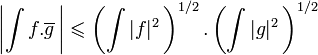 .
.Autres applications [modifier]
On la retrouve aussi dans le théorème de Lax-Milgram.
En théorie des probabilités toujours, dans l'espace des variables aléatoires admettant un moment d'ordre 2, l'inégalité de Cauchy-Schwarz fournit l'inégalité  , qui compare l'espérance du produit de deux variables aléatoires au produit des espérances de leurs carrés8. Elle permet d'établir que le coefficient de corrélation de deux variables aléatoires est un réel compris entre -1 et 19.
, qui compare l'espérance du produit de deux variables aléatoires au produit des espérances de leurs carrés8. Elle permet d'établir que le coefficient de corrélation de deux variables aléatoires est un réel compris entre -1 et 19.
Généralisation [modifier]
 un espace vectoriel réel (resp. complexe) muni d'une forme bilinéaire symétrique positive (resp. d'une forme hermitienne positive). Alors, pour tous vecteurs x et y de E,
un espace vectoriel réel (resp. complexe) muni d'une forme bilinéaire symétrique positive (resp. d'une forme hermitienne positive). Alors, pour tous vecteurs x et y de E,
 est positive et non dégénérée, et montrons qu'elle est définie. Soit x un vecteur dont la semi-norme est nulle. Le théorème 2 montre que pour tout vecteur y on a
est positive et non dégénérée, et montrons qu'elle est définie. Soit x un vecteur dont la semi-norme est nulle. Le théorème 2 montre que pour tout vecteur y on a 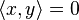 , donc, par non dégénérescence, x = 0.
, donc, par non dégénérescence, x = 0.Références [modifier]
Notes et références [modifier]
 , selon qu'on applique le théorème 1 énoncé en début d'article ou le théorème 2 du paragraphe Généralisation.
, selon qu'on applique le théorème 1 énoncé en début d'article ou le théorème 2 du paragraphe Généralisation.Liens externes [modifier]
Bibliographie [modifier]
22:28 Publié dans Inégalité de Cauchy-Schwarz | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook







































