17/04/2011
Chronologie de l'algèbre
Chronologie de l'algèbre
Aller à :Navigation,rechercher
Le tableau de cette page fournit une chronologie sommaire des mots clefs dans le développement de l'algèbre. Le découpage en grande période tient compte de l'avancée des mathématiques dans le monde gréco-latin, arabo-musulman, et européen. Il ne prétend pas rendre compte du mouvement général, Inde et Chine comprises, du développement d'ensemble des notions algébriques.
|
Année |
Évènement |
|
|
|
|
Les origines de l'algèbre. |
|
|
|
|
|
Vers le XVIIIe siècle av. J.-C. |
Les scribes babyloniens recherchent la solution d'une équation quadratique. Voir Tablette de Strasbourg |
|
Vers le XVIIIe siècle av. J.-C. |
La tablette Plimpton 322 écrite à Babylone en écriture Cunéiforme donne une table de triplets pythagoriciens. |
|
Vers le VIIIe siècle av. J.-C. |
Le mathématicien indien Baudhayana, dans son Baudhayana Sulba Sutra, découvre les triplets pythagoriciens de façon algébrique et une solution géométrique des équations linéaires et des équations quadratiques de la forme ax2 = c and ax2 + bx = c, enfin, il trouve deux ensembles de solutions entières et positives à un système d'équations diophantiennes. |
|
Vers le VIIe siècle av. J.-C. |
Le mathématicien indien Apastamba, dans son Apastamba Sulba Sutra, résout les équations linéaires générales et utilise les systèmes d'équations diophantiennes comportant jusqu'à cinq inconnues. |
|
Vers le IVe siècle av. J.-C. |
Dans le livre II de ses Éléments, Euclide donne une construction géométrique à la règle et au compas de la solution d'une équation quadratique pour des racines réelles et positives. La construction est un résultat de l'école de géométrie de Pythagore. |
|
Vers le IVe siècle av. J.-C. |
Une construction géométrique de la solution des équations cubiques est soulevée (le problème de la duplication du cube). Il est connu que celui-ci n'a pas de solution constructible à la règle et au compas. |
|
Vers 150 |
Le mathématicien grec Héron d'Alexandrie traite des équations algébriques dans ses trois volumes de mathématiques. |
|
|
|
|
De Diophante à Al-Khwarizmi, l'algèbre se dégage de la géométrie. |
|
|
|
|
|
Vers 200 |
Le mathématicien hellénistique Diophante qui vécut à Alexandrie, et souvent considéré comme le père de l'algèbre, écrit son fameux Arithmetica, un travail préfigurant la théorie des équations algébriques et la théorie des nombres. |
|
Vers 300 |
Des équations algébriques sont traitées dans le manuel chinois de mathématiques de Liu Hui Jiuzhang suanshu (The Nine Chapters on the Mathematical Art), qui contient la solution de systèmes linéaires utilisant la méthode de la fausse position, des solutions géométriques d'équations quadratiques et la recherche de matrices équivalentes selon la méthode de Sylvester-Gauss. |
|
Le mathématicien indien Aryabhata, dans son traité Aryabhatiya, obtient le nombre complet de solutions d'un système d'équations linéaires par des méthodes équivalentes aux méthodes modernes, et décrit la solution générale de telles équations. Il donne également des solutions d'équations différentielles. |
|
|
Vers 625 |
Le mathématicien chinois Wang Xiaotong trouve les solutions numériques d'une équation cubique. |
|
Le mathématicien indien Brahmagupta, dans son traité Brahma Sputa Siddhanta, invente la méthode du chakravala pour résoudre les équations quadratiques, dont l'équation de Pell, et donne des règles pour résoudre les équations linéaires et quadratiques. Il découvre que les équations du second degré ont deux racines, dont les négatives et les irrationnelles. |
|
|
Vers 800 |
Les califes abbassides al-Mansur, Haroun ar-Rachid, et Al-Mamun, ont fait traduire les travaux scientifiques des Grecs, des Babyloniens et des Indiens en langue arabe. Commence ainsi, au Moyen-Orient, une renaissance de la culture scientifique. Bagdad devient une nouvelle Alexandrie, particulièrement sous le règne d'Al-Mamun (809-833). À la suite d'un rêve où lui serait apparu Aristote, le calife a demandé à ce qu'on traduise tout ce qu'on connaissait des Grecs, y compris l'Almageste de Ptolémée et une version complète des éléments d'Euclide. Al-Mamun fit construire à Baghdad une « Maison de la Sagesse » (Bait al-hikma) afin de rivaliser avec l'ancien Museum d'Alexandrie. |
|
|
|
|
D'Al-Khawarizmi à Stevin, l'algèbre établit ses procédures. |
|
|
|
|
|
Le mot algèbre naît. Il dérive de l'opération qui consiste à diviser les deux membres d'une égalité par une même quantité (non nulle). Il ne peut être séparé qu'au prix d'une mutilation du terme « Al'muqabala », (transposition) aujourd'hui inusité, qui désigne la soustraction aux deux membres d'une même quantité. Ces deux termes forment le projet algorithmique décrit par Muḥammad ibn Mūsā al-Ḵwārizmī dans Al-Kitab al-Jabr wa-l-Muqabala (soit « La méthode de calcul par réduction et transposition » ou restauration et comparaison). On obtient ainsi la solution des équations linéaires. Al-Khwarizmi est souvent considéré comme le père de l'algèbre médiévale, car il dégage celle-ci de l'emprise géométrique. |
|
|
Vers 850 |
Le mathématicien persan Al-Mahani (en) conçoit l'idée de réduire géométriquement le problème de la duplication du cube à un problème algébrique. |
|
Vers 850 |
Le mathématicien indien Mahavira résout différentes équations paramétrées de degrés élevés. |
|
Vers 990 |
Le mathématicien persan Al-Karaji (ou al-Karkhi), dans son ouvrage l'Al-Fakhri, développe la méthode d'Al-Khwarizmi. Il définit les monômes x, x2, x3, ... et 1/x, 1/x2, 1/x3, ... Il donne des règles qui régissent le produit de ceux-ci. Il découvre la première solution des équations de la forme ax2n + bxn = c. |
|
Vers 1050 |
Le mathématicien chinois Jia Xian (en) trouve des solutions numériques d'équations de degrés élevés. |
|
Le mathématicien persan Omar Khayyam donne une classification complète des équations cubiques aux racines positives et une solution géométrique lorsqu'elles sont exprimables au moyen d'intersections de coniques. Le « fabricant de tentes » résout géométriquement des équations de degré 3. Mais croit impossible leur résolution algébrique générale. Il généralise les méthodes, déjà utilisées par Menechme, Archimede, et Al'hazan, à toutes les équations de degré 3 possédant des racines positives. |
|
|
Le mathématicien indien Bhaskara, dans son ouvrage Bijaganita (Algebra), reconnaît les racines carrées négatives, résout des équations quadratiques à plusieurs inconnues, des équations d'ordre supérieur comme celles de Fermat ainsi que les équations du second degré générales. |
|
|
Vers 1200 |
Sharaf al-Dīn al-Tūsī (1135-1213) écrit l'Al-Mu'adalat (Traité des Équations), qui fournit huit types d'équations cubiques aux solutions positives et cinq types éventuellement privés de telles solutions. Il utilise ce qui deviendra la « méthode de Ruffini et Horner », méthode d'analyse numérique pour approcher les racines. Il développe les concepts d'extremum . Il entrevoit le rôle du discriminant des équations cubiques et utilise pour la première fois la formule de Cardan due à Scipione del Ferro pour résoudre les équations de degré 3. Roshdi Rashed, affirme que Sharaf al-Din découvrit la dérivée du polynôme de degré 3 et comprit la nécessité de lier cette dérivée aux conditions de résolution de cette équation. |
|
Au XIIe siècle |
Une équipe de traducteurs sous la direction de Gondisalvius traduit les manuscrits arabes de la bibliothèque de Cordoue. parmi eux, se distingue nettement un des premiers algébristes occidentaux Jean Hispalensis. Dans le même mouvement, Jordan de Nemore introduit dans son Isagogue la notations des inconnus par des symboles. |
|
En 1202 |
L'algèbre arabe conquiert l'Europe au travers du livre du Pisan Leonardo Fibonacci et de son livre Liber Abaci. |
|
En 1299 |
Le mathématicien chinois Zhu Shijie résout les équations quadratiques, numériquement des quartiques et des équations avec plusieurs inconnues (au plus 4). Il donne le premier la méthode de développement des polynômes nommé Méthode de Horner. |
|
Vers 1400 |
Jamshīd al-Kāshī développe une première forme de la méthode de Newton Regula falsi. |
|
Vers 1400 |
Le mathématicien indien Madhava de Sangamagrama trouve la solution de fonctions transcendantales et d'équations différentielles par itération. |
|
Le mathématicien arabe Abū al-Hasan ibn Alī al-Qalasādī donne une première étape de notation symbolique. |
|
|
Vers 1500 |
Le mathématicien italien Scipione del Ferro, élève de Pacioli parvient pour la première fois à une résolution algébrique d'un grand type d'équations du troisième degré. Il ne les publie pas. |
|
Le mathématicien allemand Christoff Rudolff introduit la notation des racines carrées dans son ouvrage Die Coss. |
|
|
Vers 1530 |
Robert Recorde introduit le signe = et Michael Stifel développe une première forme de notation algébrique. |
|
Niccolo Fontana Tartaglia retrouve les formules de Scipione del Ferro. |
|
|
Cardan, aidé de son secrétaire Ludovico Ferrari, publie dans son Ars magna les formules qu'il a achetées à Tartaglia sous le sceau du secret ainsi que celles recueillies dans un carnet du défunt Scipione del Ferro. Ferrari donne la solution des équations de degré 4. |
|
|
Rafaelle Bombelli donne une formulation des nombres complexes et les règles de calculs effectifs. Une racine carrée de -1 apparaît sous la forme piu di meno. |
|
|
Le mathématicien néerlandais Stevin rédige un manuel de seize pages pour populariser l'art de compter avec les nombres décimaux. Il écrit les puissances du dixième cernées d'un exposant. Il donne la première écriture des vecteurs. |
|
|
|
|
|
De Viète à Gauss, l'algèbre triomphe des équations polynomiales. |
|
|
|
|
|
Le mathématicien français François Viète ouvre une nouvelle période de l'algèbre en faisant opérer les calculs sur des lettres, voyelles pour désigner les inconnues et consonnes pour les paramètres. C'est l'algèbre nouvelle. Par cet acte fondateur, il inaugure la période qui voit triompher le formalisme dans la résolution des équations algébriques. Par ailleurs, il donne le développement du binôme de Newton, résout une équation de degré 45[réf. nécessaire] et introduit l'usage des parenthèses In artem analyticam isagoge. |
|
|
Période de diffusion de l'algèbre nouvelle grâce aux éditions de François Viète par Marin Ghetaldi, Alexander Anderson et Van Schooten. |
|
|
Le mathématicien anglais Thomas Harriot introduit, dans une publication posthume, les symboles > et <. La même année William Oughtred donne pour la première fois le symbole multiplié. |
|
|
Le philosophe et mathématicien français René Descartes renomme les inconnus x,y,z et les paramètres a,b,c et étend l'usage de l'algèbre aux longueurs et au plan, créant avec Pierre de Fermat la géométrie analytique. |
|
|
Le philosophe et mathématicien français Blaise Pascal nomme ordonnée la coordonnée portée sur le second axe du plan. |
|
|
Le philosophe et mathématicien allemand Gottfried Leibniz développe le maniement du calcul symbolique par des règles qu'il nomme characteristica generalis. Il définit les courbes algébriques et nomme abscisse la première coordonnée. Enfin, il résout les systèmes linéaires en usant - sans justification théorique - de matrices et de déterminants. |
|
|
Vers 1680 |
Isaac Newton développe le calcul formel sur les séries entières, et calcule lescontacts des branches d'une courbe algébrique par la méthode du polygone qui porte son nom. |
|
Le mathématicien japonais Kowa Seki, dans sa Méthode de résolution des problèmes cachés, découvre les premières version du déterminant. Il résout des équations de degré 4 et 5 et donne les formules de résolution des équations cubiques. |
|
|
Le mathématicien suisse Leonhard Euler donne la résolution des équations cubiques de façon achevée. |
|
|
L'encyclopédiste français Jean le Rond D'Alembert donne la première preuve du théorème fondamental de l'algèbre. |
|
|
Le mathématicien français Gabriel Cramer, dans son traité Introduction à l'analyse des courbes algébriques, établit la règle de Cramer et étudie les courbes algébriques, des systèmes qu'on nommera matriciels à l'aide de « déterminants ». |
|
|
Le mathématicien français Bézout publie ses travaux sur le degré des équations et la théorie des équations algébriques. Donnant une première preuve reliant le degré et l'intersection. |
|
|
Le mathématicien italien Paolo Ruffini démontre partiellement l'impossibilité de résoudre par radicaux toutes les équations de degré cinq. |
|
|
Le mathématicien allemand Gauss donne un démonstration rigoureuse du théorème de d'Alembert. Il commence la publication des disquisitiones qui contiennent la première preuve de la loi de réciprocité quadratique dans la partie IV)1 . |
|
|
Le mathématicien suisse Argand publie la première représentation plane des nombres complexes et utilise des mesures algébriques. |
|
|
Le mathématicien français Gergonne introduit le symbole marquant l'inclusion. |
|
|
vers 1820 |
Le mathématicien français Adrien-Marie Legendre donne par son symbole la caractérisation des résidus de carrés dans les anneaux de congruence. |
|
Le mathématicien français Jean-Victor Poncelet fonde la géométrie projective. |
|
|
Le mathématicien norvégien Niels Henrik Abel donne un exemple d'équation de degré cinq insoluble par radicaux. Il introduit la notion de nombres algébriques (publié en 1826) |
|
|
Le mathématicien allemand Möbius introduit le calcul barycentrique oublié depuis le Suisse Paul Guldin et Archimède. |
|
|
Gauss donne une construction rigoureuse des nombres complexes. |
|
|
|
|
|
|
|
|
La Théorie de Galois, développée par le mathématicien français Évariste Galois ouvre le champ d'une nouvelle ère, celle des structures. Des prémisses de la théorie des groupes sont à rechercher chez Hudde (1659), Saunderson (1740) Le Sœur (1748) et Waring (1762- 1782), Lagrange (1770 - 1771) etVandermonde (1770). Mais Évariste Galois signe véritablement l'apparition de la notion de groupe dans son travail, mal reconnu, où se trouvent les conditions nécessaires et suffisantes pour qu'une équation soit résoluble par radicaux. |
|
|
Le baron français Cauchy établit une première théorie des déterminants. Il diagonalise les endomorphismes symétriques réels dans des cas simples. |
|
|
Le géomètre français Michel Chasles introduit le terme de birapport, d'homothétie et d'homographie, notions oubliées depuis Girard Desargues. |
|
|
Le mathématicien allemand Hermann Grassmann définit le premier une notion d'algèbre, méconnue à son époque, mais qui aura l'heur d'être comprise quelques vingt ans plus tard par Sophus Lie. À la même date, l'irlandais William Rowan Hamilton définit des espaces de vecteurs. La notion d'espace vectoriel sera clairement définie par l'Allemand Möbius et par l'Italien Giuseppe Peano 40 ans plus tard. |
|
|
Énoncé de la conjecture diophantienne d'Eugène Charles Catalan. |
|
|
Publication par Liouville des travaux d'Évariste Galois (Liouville, Vol. XI). |
|
|
Le mathématicien allemand Ernst Kummer parvient à démontrer le théorème de Fermat pour tous les nombres premiers réguliers et dégage la théorie des idéaux premiers, il approfondit la décomposition des groupes. |
|
|
Publication par le mathématicien irlandais George Boole des lois de la pensée où l'analyse logique est automatisée via une structure d'algèbre. |
|
|
Vers 1850 |
Les mathématiciens anglais Arthur Cayley et James Joseph Sylvester introduisent le terme de matrices. |
|
Le mathématicien allemand Richard Dedekind introduit les termes d'anneaux et de corps dans son livre Lehrbuch des Algebra. |
|
|
Le mathématicien français Victor Puiseux développe ses séries, permettant ainsi une meilleure approche des singularités d'une courbe et l'étude de branches conjuguées 2. Un lemme de préparation de Karl Weierstrass, publié en 1895, justifiera ultérieurement cette approche. |
|
|
Le mathématicien français Liouville montre l'existence d'une infinité de nombres transcendants. |
|
|
Le mathématicien allemand Leopold Kronecker confirme les résultats de Niels Abel et d'Évariste Galois. Les travaux de Arthur Cayley font de même l'année suivante. |
|
|
Démonstration par le mathématicien allemand Gustav Roch du théorème de Riemann-Roch reliant le degré et le genre d'une courbe algébrique dans une première version analytique. |
|
|
Les mathématiciens allemands Siegfried Heinrich Aronhold et Alfred Clebsch travaillent sur les théories de l'invariant. Ils sont à l'origine de la vision algébrique des théories de Riemann, et donc les ancêtres de la cohomologie algébrique. |
|
|
Le mathématicien français Camille Jordan montre l'invariance à ordre près de la suite des groupes quotients dans la décomposition des groupes. Son travail se prolonge par ceux de Eugen Netto (1882) et de Von Dyck (1882) qui définit les groupes dans leur sens actuel. |
|
|
Le mathématicien allemand Felix Klein, dans son programme d'Erlangen, met l'étude des groupes au centre de la définition des différentes géométries. |
|
|
Le mathématicien français Charles Hermite démontre la transcendance de e. Théorème d'Hermite-Lindemann. |
|
|
Le mathématicien allemand Max Noether donne des théorèmes d'existence de courbes algébriques dans certains faisceaux de courbes. L'anglais William Kingdon Clifford étudie les algèbres qui portent son nom et seront un des objets féconds du siècle suivant. |
|
|
Le mathématicien allemand Cantor jette les bases de la théorie des ensembles et des cardinaux. Il montre que les nombres algébriques sont en fait dénombrables. |
|
|
Le mathématicien allemand Ferdinand Georg Frobenius donne la première démonstration correcte du théorème de Cayley-Hamilton. Il enrichit, par ailleurs, la théorie de la réduction et des algèbres (associatives). |
|
|
Vers 1880 |
Le mathématicien français Émile Picard étudie les surfaces algébriques, les générateurs des complexes linéaires et les groupes de diviseurs qui portent son nom. |
|
Les mathématiciens anglais William Burnside, norvégien Ludwig Sylow (82), américain Leonard Eugene Dickson (91), allemand Otto Hölder, français Emile Mathieu et allemand Heinrich Weber complètent la théorie des groupes linéaires et des groupes finis. |
|
|
Les mathématiciens italiens Castelnuovo et Federigo Enriques collaborent sur les surfaces, les classent en cinq types, et découvrent les théorèmes qui portent leur nom sur les systèmes linéaires. |
|
|
L'étude systématique des groupes s'amplifie avec le mathématicien norvégien Sophus Lie, l'allemand Issai Schur et le français Elie Cartan. Ce dernier introduit la notion de groupe algébrique. |
|
|
L'étude des groupes discrets se poursuit avec Felix Klein, Sophus Lie, Henri Poincaré, Émile Picard, en liaison avec la monodromie. |
|
|
Le mathématicien français Elie Cartan publie sa thèse sur les groupes de transformations. Il s'intéressera ultérieurement aux algèbres associatives et aux espaces symétriques. |
|
|
Le mathématicien allemand Holder montre l'isomorphisme des groupes quotients entrant dans les tours de décompositions. |
|
|
Le mathématicien italien Giuseppe Peano introduit le symbole d'appartenance ainsi qu'une première version de l'écriture des quantificateurs. Leur forme définitive sera donnée par David Hilbert. Il donne plus de 40000 définitions dans une langue qu'il veut universelle. |
|
|
|
|
|
De David Hilbert à Kurt Gödel, l'algèbre des structures complexes. |
|
|
|
|
|
Le mathématicien allemand David Hilbert donne une première approche du corps de classe. Dans sa conférence 1900, lors du deuxième congrès international de mathématiques tenu à Paris, il présente les 21 problèmes de Hilbert, dont une partie porte sur la théorie de la démonstration et l'algèbre. On retiendra notamment le troisième qui débouche sur le paradoxe de Banach-Tarski, le cinquième, le huitième (qui demeure ouvert), le quinzième (qui appelle la théorie de l'intersection). Ils sont de natures plus ou moins profondes, mais ils ont fortement influé sur les mathématiques du siècle. |
|
|
Les travaux concernant les automorphismes des groupes de grande dimension sont poursuivis par Moore, William Burnside et vulgarisés par Leonard Eugene Dickson3. |
|
|
Le rôle des groupes simples est développé par le Français Camille Jordan. Des critères de non-simplicité le sont par l'Allemand Otto Hölder, qui classifie 200 groupes non triviaux. On atteint avec l'Américain Frank Nelson Cole le nombre de 660, avec l'Anglais William Burnside 1092 (2001 de nos jours par l'Américain Gary Lee Miller) 4. |
|
|
Le mathématicien allemand Anton Suschkewitsch et le Français Jean-Armand De Seguier (1862-1935)5 fondent la théorie des semi-groupes. |
|
|
Vers 1910 |
Les travaux de Walther von Dyck, l'Allemand Max Dehn (1900-1910), le Danois Jakob Nielsen 6 complètent la théorie des groupes. |
|
Le mathématicien français Albert Châtelet travaille sur les automorphismes des groupes abéliens. |
|
|
Collaboration des mathématiciens anglais J.E. Littlewood et G. H. Hardy avec le mathématicien indien S. Ramanujan. |
|
|
Le mathématicien français Gaston Julia décrit les formes binaires non quadratiques. L'allemand Erich Hecke étudie l'équation fonctionnelle de la fonction zêta de Dedekind, manie les fonctions thêta et certains caractères de fonctions L nommés d'après son nom. |
|
|
Création des algèbres de Von Neumann. |
|
|
Hermann Weyl développe ses travaux sur les groupes compacts. |
|
|
Travaux de l'anglo-canadien Coxeter en combinatoire et en théorie des groupes permettant d'unifier les groupes décrits par Hermann Weyl. |
|
|
Le mathématicien japonais Teiji Takagi7 livre les premiers résultats fondamentaux sur le corps de classe. |
|
|
Louis Mordell a démontré que l'ensemble des points rationnels d'une courbe elliptique forme un groupe abélien de type fini. Il est à l'origine de la conjecture de Mordell-Weyl, qu'établira Gerd Faltings en 1983. |
|
|
Heinz Hopf démontre que toute variété Riemannienne de dimension 3 de courbure constante est globalement isométrique à un espace euclidien, sphérique ou hyperbolique. Il donne une nouvelle démonstration au théorème de Poincaré-Hopf. Les notions qu'il introduit marquent la naissance des Algèbres de Hopf. |
|
|
Le mathématicien allemand Helmut Hasse publie sa théorie des corps de nombres algébriques. Son compatriote Richard Brauer commence à développer le travail dans les algèbres qui portent son nom. |
|
|
Le mathématicien autrichien Artin publie la théorie de la loi de réciprocité générale. |
|
|
Le mathématicien français André Weil étudie l'arithmétique des courbes algébriques. |
|
|
La mathématicienne allemande Emmy Noether fixe la théorie des hypercomplexes ou algèbres associatives. |
|
|
Parution de la Moderne Algebra de Van der Warden. Le mathématicien hollandais résout le quinzième problème de Hilbert en définissant une vraie théorie de l'intersection dans le groupe des diviseurs d'une variété algébrique. |
|
|
Vers 1930 |
Le mathématicien anglais Raymond Paley démontre l'existence de matrices de Hadamard d'ordre q+1 lorsque q est une puissance d'un nombre premier congrue à 3 modulo 4. Il fonde ainsi la conjecture d'Hadamard. |
|
Le mathématicien allemand Wolfgang Krull développe la théorie des idéaux maximaux. |
|
|
Le mathématicien français Claude Chevalley étudie les corps de classe des corps finis et les corps locaux. Il introduit les adèles et les idèles. Son camarade André Weil fonde ce qui deviendra la Cohomologie Galoisienne. |
|
|
Naissance de Nicolas Bourbaki sous l'impulsion d'André Weil, d'Henri Cartan, de Claude Chevalley, de Jean Delsarte8, de Jean Dieudonné, de Charles Ehresmann, de René de Possel et de Szolem Mandelbrojt |
|
|
Le mathématicien polonais Tarski poursuit les travaux de logique à propos de la complétude de l'algèbre et des théorèmes de transfert. Il montre l'indécidabilité de la théorie des groupes. C'est le théorème de Tarski. Il retrouve ainsi les résultats non publiés du très cosmopolite Kurt Gödel (1931). |
|
|
Le mathématicien russe Andreï Kolmogorov définit son travail topologique en terme cohomologique. |
|
|
Oscar Zariski définit la topologie de Zariski sur les variétés algébriques. |
|
|
|
|
|
De Bourbaki à Andrew Wiles, l'algèbre de la cohomologie, des catégories et des schémas. |
|
|
|
|
|
Travaux du mathématiciens français Pierre Samuel sur la multiplicité. |
|
|
Les Américains Samuel Eilenberg et Saunders Mac Lane fondent la notion de catégorie. |
|
|
Le mathématicien américain John Tate donne une nouvelle forme de cohomologie. |
|
|
Les séminaires Cartan, rue d'Ulm, conduisent le mathématicien français Henri Cartan et Samuel Eilenberg à la publication de Homological Algebra (1956). L'étude chomologique du corps de classe conjoint les efforts des mathématiciens français Claude Chevalley, de Jean-Louis Koszul et de Jean-Pierre Serre. |
|
|
Publication des livres de Pierre Samuel. |
|
|
La conjecture de Shimura-Taniyama-Weil annonce que toute courbe elliptique est associée à une forme modulaire de même fonction L. Une version faible est annoncée par le mathématicien japonais Yutaka Taniyama. Elle est reformulée par André Weil dans les années 1960. |
|
|
Le mathématicien ukrainien Oscar Zariski utilise les surfaces qui portent son nom pour obtenir des surfaces non rationnelles mais unirationnelles. Le problème de l'unirationnalité demeure ouvert même pour des surfaces simples 9. |
|
|
Vers 1960 |
L'Américain John Griggs Thompson accomplit des progrès décisifs dans la classification des groupes finis. |
|
Vers 1960 |
Le mathématicien japonais Kunihiko Kodaira achève ses travaux par un renouvellement de la classification des surfaces algébriques. |
|
Le mathématicien anglais David Mumford rénove dans le langage des schémas les points de vue de Kodeira sur la classification des surfaces dans l'American Journal of Mathematics ; notamment en caractéristique p. |
|
|
Le mathématicien français Yves Hellegouarch étudie les propriétés de courbes elliptiques associées à des contre-exemples au dernier théorème de Fermat. Il fonde l'étude des formes modulaires. |
|
|
Le mathématicien français Alexandre Grothendieck développe et pousse à son terme la théorie des catégories et des schémas. |
|
|
Énoncé par le mathématicien canadien Robert Langlands du Programme de Langlands qui permet de lier la généralisation des fonctions L de Dirichlet dans le cas des groupes de Galois non-abéliens aux représentation cuspidale automorphes. Travail initialisé par Israel Gelfand. |
|
|
Vers 1980 |
Le mathématicien français Alain Connes résout une grande part des problèmes soulevés par la théorie des algèbres de Von Neumann, notamment la classification des facteurs de type III. Pour cela, il sera récompensé parla médaille Fields en 1982. |
|
Vers 1980 |
Le mathématicien russe Yuri Manin établit une part de la conjecture de Mordell et, avec Iskovskikh, un contre exemple à la conjecture de Lüroth. |
|
Gerd Faltings montre le Théorème de Faltings précédemment connu sous le nom de conjecture de Mordell. Il donne des résultats sur le nombre de solutions d'une équation diophantienne. |
|
|
Le mathématicien russe Vladimir Drinfeld donne forme au groupe quantique et généralise la notion d'algèbre de Hopf. |
|
|
Les travaux du mathématicien anglais Andrew Wiles, rectifiés par Richard Taylor montrent une grande partie de la conjecture de Shimura-Taniyama-Weil. Ils étendent ainsi les classes de courbes où la conjecture de Birch et Swinnerton-Dyer est vérifiée et font tomber le Dernier théorème de Fermat. |
|
|
Le mathématicien français Laurent Lafforgue démontre une partie des conjectures de Langlands. |
|
|
Démonstration de la conjecture de Shimura-Taniyama-Weil par Christophe Breuil, Brian Conrad, Fred Diamond, et Richard Taylor. |
|
|
Le mathématicien russe Vladimir Voevodsky développe la notion d'homotopie pour les variétés algébriques ainsi que la cohomologie motivique, faisant tomber conjecture de Milnor. |
|
|
Une matrice de Hadamard d'ordre 428 a été donnée le 21 juin 2004 par Hadi Kharaghani et Behruz Tayfeh-Rezaie. Le plus petit ordre multiple de 4 pour lequel aucune matrice de Hadamard n'est connue est actuellement 668. |
Notes et références[modifier]
- ↑ La loi de réciprocité quadratique [archive] sur le site DynaMaths
- ↑ [1] Une approche des séries de Puiseux
- ↑ [2] la page Wikipédia anglaise de Leonard Dickson
- ↑ [3] [archive] le site contemporain de Gary Miller
- ↑ [4] [archive] une trace de De Seguier au travers de la biographie de Paul Dubreil (de) sur le site Chronomaths de Serge Mehl
- ↑ [5] la page Wikipédia anglaise de Jakob Nielson
- ↑ [6] [archive] Un livre en allemand sur la naissance de l'école algébriste japonaise
- ↑ [7] la page de Wikipédia allemande de Jean Delsarte
- ↑ [8] [archive] Un exemple d'étude de surface de Zariski
Catégories : Algèbre | Histoire des mathématiques | [+]
Source : http://fr.wikipedia.org/wiki/Chronologie_de_l'alg%C3%A8bre
08:03 Publié dans Algèbre, Histoire des mathématiques | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
20/11/2010
Histoire des mathématiques
L’histoire des mathématiques s'étend sur plusieurs millénaires et dans de nombreuses régions du globe allant de la Chine à l’Amérique centrale. Jusqu'au xviie siècle, le développement des connaissances mathématiques s’effectue essentiellement de façon cloisonnée dans divers endroits du globe. À partir du xixe et surtout au xxe siècle, le foisonnement des travaux de recherche et la mondialisation des connaissances mènent plutôt à un découpage de cette histoire en fonction des domaines de mathématiques.Histoire des mathématiques
L'os d'Ishango datant de plus de 20 000 ans avant notre ère est généralement cité pour être la première preuve de la connaissance des premiers nombres premiers et de la multiplication[réf. nécessaire], mais cette interprétation reste sujette à discussions[réf. nécessaire]. Il est dit que les mégalithes en Égypte au Ve millénaire avant notre ère ou en Angleterre au IIIe millénaire incorporeraient des idées géométriques comme les cercles, les ellipses et les triplets pythagoriciens[réf. nécessaire]. En 2 600 avant notre ère, les constructions égyptiennes attestent d'une connaissance précise et réfléchie de la géométrie[réf. nécessaire]. L'ethnomathématiques est un domaine de recherche à la frontière de l'anthropologie, de l'ethnologie et des mathématiques qui vise entre autres à comprendre l'essor des mathématiques dans les premières civilisations à partir des objets, instruments, peintures, et autres documents retrouvés. On attribue généralement le début de l'écriture à Sumer, dans le bassin du Tigre et de l'Euphrate ou Mésopotamie. Cette écriture, dite cunéiforme, naît du besoin d'organiser l'irrigation 1et le commerce. Conjointement à la naissance de l'écriture naissent les premières mathématiques utilitaires (économie, calculs de surface). Le premier système numérique positionnel apparaît : le système sexagésimal. Pendant près de deux mille ans, les mathématiques vont se développer dans la région de Sumer, Akkad puis Babylone. Les tablettes datant de cette période sont constituées de tables numériques et de modes d'emploi. C'est ainsi qu'à Nippur (à une centaine de kilomètres de Bagdad), ont été découvertes au xixe siècle des tablettes scolaires datant de l'époque paléo-Babylonienne (2000 av. J.-C.)2. On sait donc qu'ils connaissaient les quatre opérations mais se sont lancés dans des calculs plus complexes avec une très grande précision, comme des algorithmes d'extraction de racines carrées3, racines cubiques, la résolution d'équations du second degré. Comme ils faisaient les divisions par multiplication par l'inverse, les tables d'inverse jouaient un grand rôle. On en a retrouvé avec des inverses pour des nombres à six chiffres sexagésimaux, ce qui indique une très grande précision 4. On a également retrouvé des tablettes sur lesquelles figurent des listes de carrés d'entier, des listes de cubes et une liste souvent interprétée comme celle de triplets pythagoriciens5 suggérant qu'ils connaissaient la propriété des triangles rectangles plus de 1 000 ans avant Pythagore. Des tablettes ont aussi été retrouvées décrivant des algorithmes pour résoudre des problèmes complexes 6. Ils étaient capables d'utiliser des interpolations linéaires pour les calculs des valeurs intermédiaires ne figurant pas dans leurs tableaux. La période la plus riche concernant ces mathématiques est la période de Hammurabi (xviiie siècle av. J.-C.). Vers 1000 av. J.-C., on observe un développement du calcul vers l'astronomie mathématique7. Les meilleures sources sur les connaissances mathématiques en Égypte antique sont le Papyrus Rhind (seconde période intermédiaire, xxe siècle av. J.-C.) qui développe de nombreux problèmes de géométrie, et le Papyrus de Moscou (1850 avant J.-C.) et le rouleau de cuir. À ces documents s'ajoutent trois autres papyrus et deux tablettes de bois ; le manque de documents ne permet pas d'attester ces connaissances8. Les Égyptiens ont utilisé les mathématiques principalement pour le calcul des salaires, la gestion des récoltes, les calculs de surface et de volume et dans leurs travaux d'irrigation et de construction (voir Sciences Égyptiennes). Ils utilisaient un système d'écriture des nombres additionnel (numération égyptienne). Ils connaissaient les quatre opérations, étaient familiers du calcul fractionnaire (basé uniquement sur les inverses d'entiers naturels) et étaient capables de résoudre des équations du premier degré par la méthode de la fausse position. Ils utilisaient une approximation fractionnaire de π9. Les équations ne sont pas écrites, mais elles sous-tendent les explications données. La source principale la plus ancienne de nos connaissances sur les mathématiques chinoises provient du manuscrit de Zhoubi Suanjing ou Les neuf chapitres sur l'art mathématique, daté du ier siècle, mais regroupant des résultats probablement plus anciens. On y découvre que les Chinois avaient développé des méthodes de calcul et de démonstration qui leur étaient propres : arithmétique, fractions, extraction des racines carrées et cubiques, mode de calcul de l'aire du disque, volume de la pyramide et méthode du pivot de Gauss. Leur développement des algorithmes de calcul est remarquablement moderne. Mais on trouve aussi, sur des os de moutons et de bœufs, des gravures prouvant qu'ils utilisaient un système décimal positionnel (numération chinoise). Ils sont aussi à l'origine d'abaques les aidant à calculer. Les mathématiques chinoises avant notre ère sont principalement tournées vers les calculs utilitaires. Elles se développent ensuite de manière propre entre le ier et le viie siècle après J.-C. puis entre le xe et le xiiie siècle. La civilisation maya s'étend de 2600 avant J.-C. jusqu'à 1500 ans après J.-C. avec un apogée à l'époque classique du iiie siècle au ixe siècle. Les mathématiques sont principalement numériques et tournées vers le comput calendaire et l'astronomie. Les Mayas utilisent un système de numération positionnel de base vingt (numération maya). Les sources mayas sont issues principalement des codex (écrits autour duxiiie siècle). Mais ceux-ci ont été en grande majorité détruits par l'Inquisition et il ne reste de nos jours que quatre codex (celui de Dresde, deParis, de Madrid et Grolier) dont le dernier est peut-être un faux. La civilisation Inca (1400-1530) a développé un système de numération positionnel en base 10 (donc similaire à celui utilisé aujourd'hui). Ne connaissant pas l'écriture10, ils utilisaient des quipus pour « écrire » les statistiques de l'État. Un quipu est un encordage dont les cordes présentent trois types de nœuds symbolisant respectivement l'unité, la dizaine et la centaine11. Un agencement des nœuds sur une corde donne un nombre entre 1 et 999 ; les ajouts de cordes permettant de passer au millier, au million, etc. La civilisation de la vallée de l'Indus développa un usage essentiellement pratique des mathématiques : système décimal de poids et mesures et régularité des proportions dans la confection de briques. Les sources écrites les plus anciennes concernant les mathématiques indiennes sont les sulba-sutras (de 800 av. J.-C. jusqu'à 200). Ce sont des textes religieux écrits en sanscrit réglementant la taille des autels de sacrifice. Les mathématiques qui y sont présentées sont essentiellement géométriques et sans démonstration. On ignore s'il s'agit de la seule activité mathématique de cette époque ou seulement les traces d'une activité plus générale. Les Indiens connaissaient le théorème de Pythagore, savaient construire de manière exacte la quadrature d'un rectangle (construction d'un carré de même aire) et de manière approchée celle du cercle. On voit apparaître aussi des approximations fractionnaires de π et de racine carrée de deux. Vers la fin de cette période, on voit se mettre en place les neuf chiffres du système décimal. Il faut ensuite attendre l'époque jaïniste (ve siècle après J.-C.) pour voir naître de nouveaux textes mathématiques. Les mathématiciens de cette époque commencent une réflexion sur l'infini, développent des calculs sur des nombres de la forme À la différences des mathématiques égyptiennes et mésopotamiennes connues par des papyrus ou des tablettes d'argiles antiques remarquablement bien conservées, les mathématiques grecques ne sont pas parvenues jusqu'à nous grâce à des traces archéologiques. On les connait grâce aux copies, traductions et commentaires de leurs successeurs. La grande nouveauté des mathématiques grecques est qu'elles quittent le domaine de l'utilitaire pour rentrer dans celui de l'abstraction. Les mathématiques deviennent une branche de la philosophie. De l'argumentation philosophique découle l'argumentation mathématique. Il ne suffit plus d'appliquer, il faut prouver et convaincre : c'est la naissance de la démonstration. L'autre aspect de ces nouvelles mathématiques concerne leur objet d'étude. Au lieu de travailler sur des méthodes, les mathématiques étudient des objets, des représentations imparfaites d'objets parfaits, on ne travaille pas sur un cercle mais sur l'idée d'un cercle. Les grandes figures de ces nouvelles mathématiques sont Thalès (-625 – -547), Pythagore (-580 – -490) et l'école pythagoricienne, Hippocrate(-470 – -410) et l'école de Chios, Eudoxe de Cnide (-408 – -355) et l'école de Cnide, Théétète d'Athènes (-415 – -369) puis Euclide. Il est probable que cette école grecque des mathématiques ait été influencée par les apports mésopotamiens et égyptiens. Ainsi Thalèsvoyagea en Égypte, et il a pu rapporter en Grèce des connaissances en géométrie. Il travailla sur les triangles isocèles et les triangles inscrits dans un cercle. Selon l'école pythagoricienne, « tout est nombre ». Les deux branches d'étude privilégiées sont l'arithmétique et la géométrie. La recherche d'objets parfaits conduit les Grecs à n'accepter d'abord comme nombres que les nombres rationnels matérialisés par la notion de longueurs commensurables : deux longueurs sont commensurables s'il existe une unité dans laquelle ces deux longueurs sont entières. L'échec de cette sélection matérialisée par l'irrationalité de la racine carrée de deux les conduit à n'accepter que les nombres constructibles à la règle et au compas. Ils se heurtent alors aux trois problèmes qui vont traverser l'histoire : la quadrature du cercle, la trisection de l'angle et la duplication du cube. En arithmétique, ils mettent en place la notion de nombre pair, impair, parfait et figuré. Cet idéalisation des nombres et le souci de les relier à des considérations géométriques est probablement lié au système de numération grecque assez peu pratique : si le système est décimal, il est additif et se prête donc assez peu facilement aux calculs numériques. En géométrie, ils étudient les polygones réguliers avec un penchant pour le pentagone régulier. Hippocrate de Chios cherchant à résoudre le problème mis en place par Pythagore découvre la quadrature des lunules et perfectionne le principe de la démonstration en introduisant la notion de problèmes équivalents. Eudoxe de Cnide travaille sur la théorie des proportions acceptant ainsi de manipuler des rapports de nombres irrationnels. Il est probablement à l'origine de la formalisation de laméthode d'exhaustion pour le calcul par approximations successives d'aires et de volumes. Théétète travaille sur les polyèdres réguliers. La synthèse la plus importante des mathématiques grecques vient des Éléments d’Euclide. Les objets géométriques doivent être définis : il ne s'agit plus d'objets imparfaits mais de l'idée parfaite des objets. Dans ses Éléments, Euclide se lance dans la première formalisation de la pensée mathématique. Il définit les objets géométriques (droites, cercles, angles), il définit l'espace par une série d'axiomes, il démontre par implication les propriétés qui en découlent et fait le lien formel entre nombre et longueur. Cet ouvrage restera dans le cursus mathématique universitaire européen jusqu'au xixe siècle. Après Euclide, d'autres grands noms éclairent les mathématiques grecques. Archimède qui perfectionne les méthodes d'Eudoxe, et Apollonius de Perge dont le traité sur les coniquesest considéré comme un classique de la géométrie grecque. Dans l'antiquité tardive, les mathématiques sont représentées par l'école d'Alexandrie. Diophante étudiera les équations dites diophantiennes, et sera appelé le "père de l'algèbre". Durant la période allant de 800 à 1500 après J.C., c'est dans les régions conquises par les musulmans que se développent le plus les mathématiques. La langue arabe devient langue officielle des pays conquis. Un vaste effort de recueils et de commentaires de textes est entrepris. S'appuyant d'une part sur les mathématiques grecques, d'autre part sur les mathématiques indiennes et chinoises que leur relations commerciales leur permettent de connaître, les mathématiciens musulmans vont considérablement enrichir les mathématiques, développant l'embryon de ce qui deviendra l'algèbre, répandant le système décimal indien avec les chiffres improprement appelés chiffres arabes et développant des algorithmes de calculs. Parmi les nombreux mathématiciens musulmans, on peut citer Al-Khwarizmi et son ouvrage al-jabr. On assiste à un développement important de l'astronomie et de la trigonométrie. Le rôle du Moyen Âge fut essentiel pour l'extension du domaine des nombres. C'est durant le Moyen Âge que l'application de l'algèbre au commerce amena en Orient l'usage courant des nombres irrationnels, un usage qui se transmettra ensuite à l'Europe. C'est aussi durant le Moyen Âge, mais en Europe, que pour la première fois des solutions négatives furent acceptées dans des problèmes. C'est enfin peu après la fin du Moyen Âge que l'on considéra les quantités imaginaires, qui permettaient de mettre en évidence des solutions réelles de certaines équations du troisième degré. Dès le xiie siècle est entreprise en Italie une traduction des textes arabes et, par là-même, la redécouverte des textes grecs12. Tolède, ancien centre culturel de l'Espagne musulmane, devient, suite à la Reconquista, l'un des principaux centres de traduction, grâce au travail d'intellectuels comme Gérard de Crémone ou Adélard de Bath. L'essor économique et commercial que connaît alors l'Europe, avec l'ouverture de nouvelles routes commerciales notamment vers l'Orient musulman, permet également aux milieux marchands de se familiariser avec les techniques transmises par les Arabes. Ainsi, Léonard de Pise, avec son Liber abaci en 1202, contribue largement à faire redécouvrir les mathématiques à l'Europe. Parallèlement au développement des sciences, se concentre une activité mathématique en Allemagne, en Italie et en Pologne aux xive siècle et xve siècle. On assiste à un développement important de l'école italienne avec Scipione del Ferro, Tartaglia, Cardan, Ferrari, Bombelli, école principalement tournée vers la résolution des équations. Cette tendance est fortement liée au développement dans les villes italiennes de l'enseignement des mathématiques non plus dans un but purement théorique tel qu'il pouvait l'être dans le Quadriviummais à des fins pratiques, notamment destinée aux marchands. Cet enseignement se diffuse dans des botteghe d'abbaco ou « écoles d'abbaques » où des maestri enseignent l'arithmétique, la géométrie et les méthodes calculatoires à de futurs marchands à travers des problèmes récréatifs, connus grâce à plusieurs « traités d'abbaque » que ces maîtres nous ont laissés13. Les nombres complexes apparaissent lors des travaux de Scipione del Ferro, à l'occasion de la résolution des équations de degrés trois. Repris par Tartaglia, et publiés par Cardan, ils trouvent une première forme avec Bombelli. Ferrari résout les équations du quatrième degré. Jusqu'à la fin du xvie siècle, la résolution de problèmes demeure cependant rhétorique. Le calcul symbolique apparaît en 1591 lors de la publication de l’Isagoge de François Viète avec l'introduction de notations spécifiques pour les constantes et les variables (ce travail popularisé et enrichi par Harriot, Fermat et Descartes modifiera entièrement le travail algébrique en Europe). Les mathématiques portent leur regard sur des aspects physiques et techniques. Fils de deux pères, Isaac Newton et Gottfried Leibniz, le calcul infinitésimal fait entrer les mathématiques dans l'ère de l'analyse (dérivée, intégrale, équation différentielle). L'univers mathématiques du début du xviiie siècle est dominé par la figure de Leonhard Euler 14 et par ses apports tant sur les fonctions que sur la théorie des nombres, tandis que Joseph-Louis Lagrange éclaire la seconde moitié de ce siècle. Le siècle précédent avait vu la mise en place du calcul infinitésimal ouvrant la voie au développement d'un nouveau domaine mathématique : l'analyse algébrique dans laquelle, aux opérations algébriques classiques, viennent s'ajouter deux opérations nouvelles, la différentiation et l'intégration (introductio in analysin infinitorum - Euler-1748). Le calcul infinitésimal se développe et s'applique aussi bien aux domaines physiques (mécanique, mécanique céleste, optique, cordes vibrantes) qu'aux domaines géométriques (étude de courbes et de surfaces).Leonhard Euler, dans Calculi différentialis (1755) et Institutiones calculi integralis (1770) essaie de mettre au point les règles d'utilisation des infiniment petits et développe des méthodes d'intégration et de résolution d'équations différentielles. Jean le Rond d'Alembert puis Joseph-Louis Lagrange lui emboîtent le pas. En 1797, Sylvestre-François Lacroix publie Traité du calcul différentiel et intégral qui se veut une synthèse des travaux d'analyse du xviiie siècle. La famille Bernoulli contribue au développement de la résolution des équations différentielles. La fonction devient un objet d'étude à part entière. On s'en sert dans des problèmes d'optimisation. On la développe en séries entières ou asymptotiques(Taylor, Stirling, Euler, Maclaurin, Lagrange), mais sans se préoccuper de leur convergence. Leonhard Euler élabore une classification des fonctions. On tente de les appliquer à des réels négatifs ou à des complexes 15. Le théorème fondamental de l'algèbre (existence de racines éventuellement complexes à tout polynôme) resté sous forme de conjecture depuis deux siècles est remis en avant dans l'utilisation de la décomposition des fractions en éléments simples nécessaire pour le calcul intégral. Successivement, Euler (1749), le chevalier de Foncenex (1759) et Lagrange (1771) tentent des démonstrations algébriques mais se heurtent à la partie transcendante du problème (tout polynôme de degré impair sur R possède une racine réelle) qui nécessiterait l'utilisation du théorème des valeurs intermédiaires16.. La démonstration de D'Alembert, publiée en 1746 dans les annales de l'académie de Berlin, est la plus achevée mais présente encore quelques trous et des obscurités. Gauss, en 1799, qui critique D'Alembert sur ces points n'est d'ailleurs pas exempté des mêmes reproches. Il faut à un moment faire intervenir un résultat d'analyse fort que le siècle ne connaît pas. De plus, l'obstacle se situe dans la question des points de branchement: on retrouve ici une question déjà débattue lors de la polémique sur les logarithmes des nombres négatifs que tranchera Euler. La seconde et la troisième démonstration de Gauss ne souffrent pas de ces reproches mais on n'est plus au xviiie siècle... En arithmétique, Euler démontre le petit théorème de Fermat et en donne une version élargie aux nombres composés (1736-1760). Il infirme la conjecture de Fermat sur la primalité des nombres de la forme Durant ce siècle, les mathématiciens continuent de s'intéresser aux résolutions algébriques des équations. Le premier essai systématique sur la résolution des équations algébriques était l'œuvre de Tschirnhaus en 1683. Euler lui-même, dans deux essais, ne va pas au-delà de son devancier et en 1762, Bezout introduit la notion de racine de l'unité. Entre 1770 et 1772, on peut citer trois grands mémoires plus originaux : celui de Waring, celui d'Alexandre-Théophile Vandermonde (1771) sur la résolubilité par radicaux des équations xn − 1 = 0(équation cyclotomique) qui est un précurseur dans l'utilisation des permutations des racines21 et celui de Lagrange (1770) qui rassemble toutes les méthodes de résolutions déjà tentées mais va introduire les résolvantes de Lagrange et démontrer, dans un langage où la notion de groupe n'existe pas encore, le théorème de Lagrange: l'ordre d'un sous-groupe d'un groupe fini divise l'ordre du groupe. Ces deux derniers mathématiciens mettent en évidence l'importance des racines et de leurs permutations mais il faut attendre le siècle suivant pour voir naitre la notion de groupe de permutations. La géométrie analytique se développe et s'étend de l'étude des courbes à celle des surfaces. Euler étudie l'équation générale du second degré à trois variables et présente une classification des solutions. Alexis Clairaut étudie les courbes gauches (1729). Gabriel Cramer publie en 1750 un traité sur les courbes algébriques. La grande figure de la géométrie du XVIIIe reste Gaspard Monge22. Celui-ci développe la géométrie différentielle avec l'étude des tangentes et crée une nouvelle discipline: la géométrie descriptive. Leonhard Euler développe le calcul trigonométrique, met en place les formules de calcul de la géométrie sphérique et replace les fonctions circulaires dans l'ensemble général des fonctions, les développant en séries entières ou en produits infinis et découvrant une relation entre les fonctions circulaires et les fonctions exponentielles Le siècle voit l'apparition de quelques théoriciens de la logique. Leonhard Euler met au point une méthode de représentation figurée des déductions syllogistiques (diagramme d'Euler), Jean-Henri Lambert travaille sur la logique des relations 22. C'est aussi le siècle qui s'attaque aux premiers exemples de ce qui va devenir la théorie des graphes. Euler résout en 1736 le problème des ponts de Königsberg, et, en 1766, énonce le théorème des circuits eulériens: un p-graphe admet un circuit eulérien si et seulement si le nombre de ses sommets de degré impair est 0 ou 2. Il s'attaque au problème du cavalier en 1759 mais ne publie rien jusqu'en 1766. Il s'agit d'un cas particulier de graphes hamiltoniens. Le problème du cavalier est connu depuis fort longtemps. Vers 840, al-Adli ar-Rumi en donne une solution. Le poête Rudrata en parlait aussi dans le Kavyalankara, un texte indou. Mais le siècle est fécond aussi en conjectures qui resteront des énigmes pendant plus d'un siècle : le problème de Goldbach, le problème de Waring23, ... Le siècle voit aussi Legendre s'échiner pendant des années sur les intégrales elliptiques. Malheureusement pour lui, même s'il fait l'admiration d'Euler en ce domaine, la solution de la question allait lui échapper au profit d'Abel. Le xviiie siècle est aussi celui de l'encyclopédie dans laquelle Jean le Rond d'Alembert fait un état des lieux des mathématiques de ce siècle. Durant la période Edo (1603 - 1887), au Japon, se développe une mathématique sans influence de la mathématique occidentale mais inspirée de la mathématique chinoise, travaillant sur des problèmes d'essence géométrique. Des énigmes géométriques sont posées et résolues sur des tablettes en bois appelées Sangaku. L'histoire mathématique du xixe siècle est riche. Trop riche pour qu'en un essai de taille raisonnable on puisse couvrir la totalité des travaux de ce siècle. Aussi ne doit-on attendre de cette partie que les points saillants des travaux de ce siècle. Le xixe siècle vit apparaître plusieurs théories nouvelles et l'accomplissement des travaux entrepris au siècle précédent. Le siècle est dominé par la question de la rigueur. Celle-ci se manifeste en analyse avec Cauchy et la sommation des séries. Elle réapparaît à propos de la géométrie. Elle ne cesse de se manifester en théorie des fonctions et particulièrement sur les bases du calcul différentiel et intégral au point de voir disparaître totalement ces infiniments petits qui avaient pourtant fait le bonheur du siècle précédent. Mais plus encore, le siècle marque la fin de l'amateurisme mathématique: les mathématiques étaient jusque là surtout le fait de quelques particuliers suffisamment fortunés soit pour étudier eux-mêmes soit pour entretenir quelques génies. Au xixe siècle, tout cela prend fin : Les mathématiciens deviennent des professionnels appointés. Le nombre de ces professionnels ne cesse de croître et avec ce nombre, les mathématiques prennent une importance jamais atteinte, comme si la société tout entière prenait enfin conscience du formidable outil. Les applications, en germe dans le siècle précédent, se développent rapidement dans tous les domaines, laissant croire que la science peut tout. D'ailleurs, certains succès sont là pour en attester. N'a-t-on pas découvert une nouvelle planète uniquement par le calcul ? N'a-t-on pas expliqué la création du système solaire ? Le domaine de la physique, science expérimentale par excellence est complètement envahi par les mathématiques: la chaleur, l'électricité, le magnétisme, la mécanique des fluides, la résistance des matériaux et l'élasticité, la cinétique chimique sont à leur tour mathématisés au point que le bon vieux cabinet de curiosité du xviiie siècle finissant est remplacé par un tableau noir. Et le vaste champ de la science s'étend encore et encore. Certes, on ne dit plus ce presque lieu commun du xviiie siècle que les sciences mathématiques seront bientôt achevées et qu'il faudra "fermer la mine", à la place on se met à rêver à la machine de Leibniz qui répondrait à toutes les questions. On va même jusqu'à quantifier le hasard ou l'incertain, histoire de se rassurer. Cournot veut appliquer le calcul des probabilités en matière judiciaire pour arriver à cette stupéfiante, et combien rassurante, conclusion qu'il y a moins de deux pour cent d'erreurs judiciaires ! Les mathématiques s'insinuent jusqu'à la structure intime de la matière: plusieurs théories de la lumière et les prémisses de la théorie de la relativité chez Lorentz qui complète la théorie électromagnétique de Maxwell. La tendance à la rigueur, commencée au début du xixe siècle, ne verra son accomplissement qu'au début du xxe siècle par la remise en cause de bien des a priori.Préhistoire [modifier]
De Sumer à Babylone [modifier]
Égypte [modifier]
Chine [modifier]
Civilisations précolombiennes [modifier]
Inde [modifier]
 qu'ils nomment première racine carrée, seconde racine carrée, troisième racine carrée. De cette époque, datent l'Aryabhata (499), du nom de son auteur, écrit en sanscrit et en vers, et les traités d'astronomie et de mathématiques de Brahmagupta (598-670) . Dans le premier, on y trouve des calculs de volume et d'aire, des calculs de sinus qui donne la valeur de la demi-corde soutenue par un arc, la série des entiers, des carrés d'entiers, des cubes d'entiers. Une grande partie de ces mathématiques sont orientées vers l'astronomie. Mais on trouve aussi des calculs de dettes et recettes où l'on voit apparaître les premières règles d'addition et de soustraction sur les nombres négatifs. Mais c'est à Brahmagupta semble-t-il que l'on doit les règles opératoires sur le zéro en tant que nombre et la règle des signes.
qu'ils nomment première racine carrée, seconde racine carrée, troisième racine carrée. De cette époque, datent l'Aryabhata (499), du nom de son auteur, écrit en sanscrit et en vers, et les traités d'astronomie et de mathématiques de Brahmagupta (598-670) . Dans le premier, on y trouve des calculs de volume et d'aire, des calculs de sinus qui donne la valeur de la demi-corde soutenue par un arc, la série des entiers, des carrés d'entiers, des cubes d'entiers. Une grande partie de ces mathématiques sont orientées vers l'astronomie. Mais on trouve aussi des calculs de dettes et recettes où l'on voit apparaître les premières règles d'addition et de soustraction sur les nombres négatifs. Mais c'est à Brahmagupta semble-t-il que l'on doit les règles opératoires sur le zéro en tant que nombre et la règle des signes.Grèce antique [modifier]
Civilisation islamique [modifier]
Occident [modifier]
Durant le Moyen Âge [modifier]
Durant la renaissance européenne [modifier]
Au xviie siècle [modifier]
Le xviiie siècle [modifier]
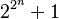 (nombre de Fermat)17. Il s'intéresse à la répartition des nombres premiers et prouve que la série des inverses des nombres premiers est divergente18. Laconjecture de Bachet (tout nombre est somme de 4 carrés au plus) est démontrée par Lagrange en 1770. C'est aussi Lagrange qui démontre en 1771 le théorème de Wilson (si p est premier, il divise (p-1)! + 1). Il développe la technique de décomposition en fractions continues et démontre l'infinité des solutions de l'équation de Pell-Fermat19. Legendre publie en 1798 sa Théorie des nombres qui rassemble un grand nombre de résultats d'arithmétique20.La loi de réciprocité quadratique conjecturée par Euler et Legendre ne sera démontrée que le siècle suivant.
(nombre de Fermat)17. Il s'intéresse à la répartition des nombres premiers et prouve que la série des inverses des nombres premiers est divergente18. Laconjecture de Bachet (tout nombre est somme de 4 carrés au plus) est démontrée par Lagrange en 1770. C'est aussi Lagrange qui démontre en 1771 le théorème de Wilson (si p est premier, il divise (p-1)! + 1). Il développe la technique de décomposition en fractions continues et démontre l'infinité des solutions de l'équation de Pell-Fermat19. Legendre publie en 1798 sa Théorie des nombres qui rassemble un grand nombre de résultats d'arithmétique20.La loi de réciprocité quadratique conjecturée par Euler et Legendre ne sera démontrée que le siècle suivant.Japon [modifier]
xixe siècle [modifier]
|
Gottlob Frege.jpg
|
Euler, dont on a commencé la publication des travaux (prévus sur cinquante ans !), s'était déjà attaqué à bien des domaines : acoustique, optique, résistance des matériaux, mécanique des fluides, élasticité, mais ces domaines étaient encore naissants. C'est Fourier, dont le premier mémoire est refusé par l'Académie des sciences de Paris, qui attaque le premier la théorie de la chaleur faisant usage de ce qui va devenir les séries de Fourier. Vers la même époque, les années 1820, Fresnel s'occupe d'optique ainsi que Bessel qui va introduire lesfonctions de Bessel. La mécanique des fluides, qui en était quasiment au stade laissé par Euler et d'Alembert, le stade des fluides parfaits, fait des progrès avec Henri Navier et George Gabriel Stokes qui s'attaquent aux fluides incompressibles puis compressibles introduisant la viscosité. L'électricité, fait ses débuts sous l'influence de Gauss, d'Ohm, de Biot, de Savartet d'Ampère mais c'est surtout le génie de Maxwell qui va embrasser la théorie dans l'une des plus belles théories du siècle, la théorie électromagnétique, qui prétend unifier l'ensemble des travaux sur l'électricité, l'optique et le magnétisme. En résistance des matériaux, les progrès sont plus modestes. On peut citer notamment Barré de Saint-Venant, Yvon Villarceau,Aimé-Henry Résal et son fils Jean Résal mais il faudra attendre le siècle suivant pour que l'élasticité fasse de décisifs progrès, d'autant qu'on ignore encore bien des propriétés du béton et plus encore le béton armé. Vers la fin du siècle, on en connaît suffisamment pour que certains se lancent dans des réalisations monumentales en acier, tels Eiffel. Trois grands problèmes éclaireront le siècle : la loi de réciprocité quadratique, la répartition des nombres premiers et le grand théorème de Fermat. Le xixe siècle offre des progrès considérables sur ses trois questions grâce aux développements d'une véritable théorie prenant le nom d'arithmétique ou de théorie des nombres et s'appuyant sur des outils abstraits et sophistiqués. sous la seule justification du développement en série de Taylor de 1/(1+x). Les mathématiciens croient encore, pour peu de temps, que la somme infinie de fonctions continues est continue, et (pour plus longtemps) que toute fonction continue admet une dérivée... Mais déjà le siècle est écoulé et, au congrès international de mathématique qui se tient, en cette année 1900, à Paris, David Hilbert présente une liste de 23 problèmes non résolus de première importance pour le siècle d'après. Ces problèmes couvrent une grande partie des mathématiques et vont prendre une part importante dans l'histoire mathématique du xxe siècle. Ce paragraphe donne un ensemble de livres de première importance, soit par leur contenu historiquement important soit pour la synthèse qu'ils constituent sur un domaine donné. L'ordre choisi est alphabétique sur le nom des auteurs. Le xxe siècle aura été un siècle extraodinairement fécond du point de vue mathématique. Trois grands théorèmes dominent tous les autres : d'une part le théorème de Gödel ; d'autre part la démonstration de la conjecture de Tanyama-Shimura qui entraîna la démonstration du grand théorème de Fermat ; enfin la démonstration des conjectures de Weil par Pierre Deligne. De nouveaux domaines de recherche sont nés ou se sont développés : les systèmes dynamiques, suite aux travaux de Poincaré, les probabilités, la topologie, la géométrie différentielle, la logique, la géométrie algébrique, suite aux travaux de Grothendieck, ...Revues de mathématiques [modifier]
Mécanique [modifier]
Physique mathématique [modifier]
Théorie des nombres [modifier]
Logique [modifier]
Géométrie [modifier]
Algèbre [modifier]
Probabilité et statistiques [modifier]
Théorie des graphes [modifier]
Analyse réelle [modifier]

 . Karl Weierstrass construit
. Karl Weierstrass construit  à partir de la notion d'« agrégats » tandis que Richard Dedekind crée
à partir de la notion d'« agrégats » tandis que Richard Dedekind crée  de la notion de coupure de l'ensemble des rationnels.
de la notion de coupure de l'ensemble des rationnels.
Analyse complexe [modifier]
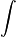 .Il démontre les inégalités "de Cauchy" qui seront intensément utilisées, dans la théorie des équations différentielles notamment.
.Il démontre les inégalités "de Cauchy" qui seront intensément utilisées, dans la théorie des équations différentielles notamment.
Perspectives [modifier]
Les livres du siècle [modifier]
xxe siècle [modifier]
La communauté mathématique explose [modifier]
Algèbre [modifier]
Mécanique [modifier]
Analyse [modifier]
Théorie des groupes [modifier]
Topologie [modifier]
Équations différentielles [modifier]
Théorie des nombres [modifier]
Graphes [modifier]
Analyse complexe [modifier]
Logique et théorie des ensembles [modifier]
Probabilités [modifier]
Analyse numérique [modifier]
Paradoxes apparents et curiosités [modifier]
Notes et références [modifier]
Voir aussi [modifier]
Liens internes [modifier]
Liens externes [modifier]
Bibliographie [modifier]
10:07 Publié dans Histoire des mathématiques | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
28/07/2010
Révolution mathématique du XVIIème siècle
Révolution mathématique du XVIIème siècleEvelyne Barbin
Le Mot de l'éditeur : Révolution mathématique du XVIIème siècle
La philosophie est écrite dans ce livre immense perpétuellement ouvert devant nos yeux (je veux dire l'univers), mais on ne peut le comprendre si l'on n'apprend pas d'abord à connaître la langue et les caractères dans lesquels il est écrit. Il est écrit en langue mathématique et ses caractères sont des triangles, des cercles, et d'autres figures géométriques, sans l'intermédiaire desquels il est humainement impossible d'en comprendre un seul mot.
Cet ouvrage propose une histoire de la révolution mathématique du XVIIe siècle, à l'intérieur de laquelle de nouvelles mathématiques ont été construites et la nature a été construite en termes mathématiques. À partir des années 1620, la science poursuit de nouveaux buts, il ne s'agit plus seulement de spéculer mais d'inventer, de résoudre des problèmes, de progresser et de maîtriser la nature. Le scientifique construit une réalité du monde à l'image de celle du monde technique, une réalité faite de quantités régies par des lois. C'est ainsi que les mathématiques vont remplacer la logique aristotélicienne dans l'étude de la nature. Les mathématiques ne sont plus purement spéculatives, mais elles sont inscrites dans la réalité du monde, elles permettent une compréhension de la réalité et une action sur elle. Ce nouveau statut appelle une transformation des mathématiques, de leurs méthodes, de leurs objets et de leurs significations. Les courbes sont les premières à être modifiées par ce nouvel enjeu. L'invention du courbe dans les années 1630-1640 désigne sans nul doute le trait le plus important de la "révolution mathématique du XVIIe siècle".
L'objet de cet ouvrage est la révolution mathématique du XVIIe siècle, non pas celle que nous pourrions définir, caractériser, décréter, à partir de cadres ou de théories a priori, mais la révolution que les acteurs mêmes disent vouloir ou non accomplir, la révolution de Bacon, Descartes, Galilée, Roberval, Fermat, Pascal, Huygens, Leibniz, Newton et de quelques autres.
Extrait du livre :
Révolution mathématique et invention du courbe
(...)
Nous ne nous satisfaisons pas de l'idée selon laquelle la mathématisation de la nature se serait imposée d'emblée à cette époque, ou du préjugé selon lequel des nouveautés mathématiques viendraient à point nommé pour s'appliquer à la nouvelle science physique. Dans cet ouvrage, nous étudions un seul et même processus historique à l'intérieur duquel les nouvelles mathématiques ont été construites et la nature a été construite en termes mathématiques.
La nouvelle science physique est nouvelle, d'abord par son questionnement. Dans la philosophie naturelle d'Aristote, il s'agissait d'expliquer les phénomènes par des causes, alors que pour le scientifique du 17ème siècle, il s'agit d'abord de comprendre des phénomènes, naturels ou artificiels, par leurs effets quantifiés et mesurés. C'est un autre questionnement sur le réel qui oriente les recherches. La science poursuit de nouveaux buts, il ne s'agit pas de spéculer mais d'inventer, de résoudre des problèmes, de progresser et de maîtriser la nature.
| Auteur | Evelyne Barbin |
|---|---|
| Editeur | Ellipses |
| Date de parution | novembre 2006 |
| ISBN | 2729831444 |
| Illustration | Pas d'illustrations |
16:20 Publié dans Histoire des mathématiques | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook



























































