02/12/2010
Glossaire de topologie
Ceci est un glossaire de quelques termes utilisés en topologie. Ce glossaire est divisé en deux parties. La première traite des concepts généraux, et la seconde liste différents types d'espaces topologiques. Dans ce glossaire, tous les espaces sont supposés topologiques.Glossaire de topologie
Sommaire[masquer] |
Accessible : voir l'axiome de séparation T1. Adhérence Base ou base d'ouverts Base de voisinages : voir Système fondamental de voisinages. Boule Cauchy : voir Suite de Cauchy. Compact : voir les axiomes de recouvrement. Complet Complètement de Hausdorff : voir l'axiome de séparation T2½. Complètement normal : voir l'axiome de séparation T5. Complètement régulier : voir l'axiome de séparation T3½. Composante connexe Connexe, connexe par arcs : voir les notions de connexité. Continu Contractile : voir les notions de connexité. Convergent Dense Dérivé Discontinu Discret Distance Engendrée : voir Topologie engendrée. Espace de Fréchet Espace de Hausdorff : voir l'axiome de séparation T2. Espace de Kolmogorov : voir l'axiome de séparation T0. Espace de Tychonoff : voir l'axiome de séparation T3½. Espace métrique Espace polonais Espace topologique Faiblement normal : voir les axiomes de séparation. Fermé Fermeture : voir Adhérence. Filtre : Un filtre sur un ensemble E est un ensemble non vide de parties non vides de E qui est stable par sur-parties et intersections finies. Dans un espace topologique, les voisinages d'un point forment un filtre. Fin Fonctionnellement séparés Fréchet : voir l'axiome de séparation T1, ou le type d'espace vectoriel topologique dit de Fréchet. Frontière Fσ : Une partie d'un espace topologique est un Fσ si c'est une réunion dénombrables de fermés. Gδ : Une partie d'un espace topologique est un Gδ si c'est une intersection dénombrables d'ouverts. Grossière : voir Topologie grossière. Hausdorff : : voir l'axiome de séparation T2 ou Séparé. Homéomorphisme Homogène Homotopie Induite : voir Topologie induite. Intérieur Isolé : voir Point isolé. Kolmogorov : voir l'axiome de séparation T0 ou Espace de Kolmogorov. Limite Lindelöf : voir l'axiome de recouvrement Espace de Lindelöf. Localement : voir Propriété locale. Maigre Métrique : voir Espace métrique. Métrisable Moins fine : voir Topologie moins fine. Normal : voir les axiomes de séparation. Ouvert Paracompact : voir les axiomes de recouvrement. Parfait Parfaitement normal : voir les axiomes de séparation. Partition de l'unité Plus fine : voir Topologie plus fine. Point d'accumulation Point isolé Polonais : voir Espace polonais. Prébase Produit : voir Topologie produit. Quasi-compact : voir les axiomes de recouvrement. Quotient Raffinement Rare Recouvrement Relativement compact Régulier : voir l'axiome de séparation T3. Séparable Séparant Séparé : voir l'axiome de séparation T2. Simplement connexe : voir les notions de connexité. Sous-recouvrement Système fondamental de voisinages Suite de Cauchy T0, T1, T2, T2½, T3, T3½, T4, T5 : voir les axiomes de séparation. Topologie Topologie discrète Topologie engendrée Topologie grossière Topologie induite Topologie moins fine Topologie plus fine Topologie produit C'est la topologie la moins fine rendant continues toutes les projections Topologie quotient Topologique : voir Espace topologique. Totalement discontinu : voir les notions de connexité. Tychonoff : voir l'axiome de séparation T3½ ou Complètement régulier. Uniformisable : dont la topologie est induite par une structure d'espace uniforme ; voir l'axiome de séparation T3½ ou Complètement régulier. Valeur d'adhérence Voisinage Les espaces topologiques peuvent être qualifiés de différentes manières en termes de séparation, de recouvrements ou de connexité. Certains des termes employés ici peuvent avoir été définis autrement dans la littérature ancienne (voir l'histoire des axiomes de séparation). T0 ou de Kolmogorov : dans lequel pour tout couple de points distincts, il existe un voisinage de l'un qui ne contient pas l'autre. T1 ou accessible ou de Fréchet : dont tous les singletons sont fermés. T2 ou de Hausdorff ou séparé : dans lequel deux points distincts admettent toujours des voisinages disjoints. T2½ ou complètement de Hausdorff : dans lequel deux points distincts admettent toujours des voisinage fermés disjoints. Régulier : séparé et dont tout point admet une base de voisinages fermés. Complètement régulier ou de Tychonoff : séparé et uniformisable, ou encore : sous-espace d'un compact. Faiblement normal : complètement régulier et dans lequel deux ouverts disjoints quelconques ont deux voisinages fermés disjoints dont l'un est à base dénombrable. Normal : séparé et dans lequel deux fermés disjoints quelconques possèdent toujours des voisinages disjoints. Le lemme d'Urysohn garantit alors que ces deux fermés sontfonctionnellement séparés. Complètement normal : dont tout sous-espace est normal. Parfaitement normal : séparé et dont tout fermé est le lieu d'annulation d'une fonction continue réelle. Les axiomes de recouvrement traitent de l'existence de raffinements ou de sous-recouvrements particuliers pour un recouvrement quelconque de l'espace considéré. Paracompact : espace séparé dont tout recouvrement ouvert admet un raffinement localement fini. Lindelöf : dont tout recouvrement ouvert admet un sous-recouvrement dénombrable. Quasi-compact : dont tout recouvrement ouvert admet un sous-recouvrement fini. Compact : quasi-compact et séparé. σ-compact ou sigma-compact : recouvert par une famille dénombrable de parties compactes. Localement compact : séparé, et dont chaque point admet un système fondamental de voisinages compacts. Séquentiellement compact : dans lequel toute suite admet au moins une valeur d'adhérence. Les hypothèses de connexité décrivent la cohésion de l'espace ou de certains voisinages, ou l'existence de déformations (homotopies) entre certaines applications continues vers l'espace considéré. Connexe : qui n'est pas l'union disjointe de deux ouverts non vides. Localement connexe : dont chaque point admet un système fondamental de voisinages connexes. Totalement discontinu : dont les seules parties connexes sont les singletons. Connexe par arcs : dont tout couple de points (x,y) est relié par un chemin (ou arc), c'est-à-dire une application continue Localement connexe par arcs : dont chaque point admet un système fondamental de voisinages connexes par arcs. Simplement connexe : connexe par arcs et dans lequel toute application continue Contractile : pour lequel l'application identité de X est homotope à une application constante.Généralités [modifier]
A [modifier]
B [modifier]
C [modifier]
D [modifier]
 satisfaisant les propriétés suivantes :
satisfaisant les propriétés suivantes :
 .
.E [modifier]
F [modifier]
L'ensemble vide et l'espace sont donc des fermés. L'union de deux fermés est un fermé et l'intersection d'une famille quelconque de fermés est un fermé.G [modifier]
H [modifier]
 est une application continue
est une application continue ![H : Xtimes [0,1] to Y](http://upload.wikimedia.org/math/e/9/0/e90fbf798237734541171ebfcd412898.png) telle que
telle que  . Les applications f et g sont alors dites homotopes.
. Les applications f et g sont alors dites homotopes.I [modifier]
K [modifier]
L [modifier]
M [modifier]
N [modifier]
O [modifier]
P [modifier]
Q [modifier]
R [modifier]
 est un recouvrement dont chaque élément est inclus dans un élément de
est un recouvrement dont chaque élément est inclus dans un élément de  .
.S [modifier]
 de voisinages de ce point tel que tout autre voisinage de ce point contient un élément de
de voisinages de ce point tel que tout autre voisinage de ce point contient un élément de  .
.T [modifier]
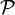 de parties d'un ensemble est celle dont les ouverts sont les réunions quelconques d'intersections finies d'éléments de
de parties d'un ensemble est celle dont les ouverts sont les réunions quelconques d'intersections finies d'éléments de 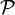 . L'ensemble
. L'ensemble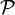 constitue une prébase de la topologie engendrée.
constitue une prébase de la topologie engendrée.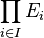 est la topologie engendrée par les
est la topologie engendrée par les  où un nombre fini d'éléments Ui sont des ouverts des espaces topologiques correspondants et les autres sont les espaces Ei correspondants.
où un nombre fini d'éléments Ui sont des ouverts des espaces topologiques correspondants et les autres sont les espaces Ei correspondants.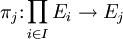 .
. une relation d'équivalence sur E, la topologie quotient sur l'ensemble quotient
une relation d'équivalence sur E, la topologie quotient sur l'ensemble quotient  est l'ensemble des parties de
est l'ensemble des parties de  dont lespréimages sont des ouverts de E. C'est la topologie la plus fine rendant continue la projection canonique, qui à tout élément de E associe sa classe d'équivalence..
dont lespréimages sont des ouverts de E. C'est la topologie la plus fine rendant continue la projection canonique, qui à tout élément de E associe sa classe d'équivalence..U [modifier]
V [modifier]
Propriétés d'espaces topologiques [modifier]
Axiomes de séparation [modifier]
Axiomes de recouvrement [modifier]
Connexité [modifier]
![p:[0,1]to X](http://upload.wikimedia.org/math/c/2/9/c2908a2ef3893f387f5f8042ee82d2b9.png) telle que p(0) = x et p(1) = y.
telle que p(0) = x et p(1) = y. est homotope à une application constante.
est homotope à une application constante.
21:39 Publié dans Glossaire, Glossaire de topologie | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
20/11/2010
Glossaire
Glossaire
Source : http://villemin.gerard.free.fr/Referenc/Vocabula/Glossair...
|
|
Nombres - Curiosités, Théorie & Usages |
||||
|
GLOSSAIRE & en savoir plus |
|||||
|
Nombres |
Maths (autre) |
Sciences |
Général |
||
|
A |
|
|||
|
B |
|
|
||
|
C |
||||
|
D |
|
|
E |
|
|||
|
F |
|
|
||
|
G |
||||
|
H |
|
|
||
|
I |
||||
|
J |
|
|
|
|
|
K |
|
|
|
|
|
L |
|
|
||
|
M |
||||
|
N |
|
|
||
|
O |
|
|||
|
P |
Pensées (citations) |
|||
|
Q |
|
|
|
|
R |
|
|||
|
S |
|
|
||
|
T |
|
|||
|
U |
|
|
|
|
|
V |
|
|||
|
WX |
|
|
|
|
|
YZ |
|
|
|
|
|
Nombres |
Maths (autre) |
Sciences |
Général |
|
Voir |
|
|
Sites |
|
Édition du 30/08/2010
Gérard Villemin
10:23 Publié dans Glossaire | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook







































