20/11/2010
Ensemble de Smith-Volterra-Cantor
En mathematiques, l'ensemble de Smith–Volterra–Cantor est un exemple de points de la droite réelle qui n'est nulle part dense (en particulier qui ne contient aucun intervalle) et qui est pourtant de mesure de Lebesgue positive. L'ensemble de Smith-Volterra-Cantor est baptisé d'après les mathématiciens Henry John Stephen Smith, Vito Volterra et Georg Cantor.Ensemble de Smith-Volterra-Cantor
Sommaire[masquer] |
De construction similaire à l'ensemble de Cantor, l'ensemble de Smith-Volterra-Cantor est construit en retirant itérativement des intervalles à l'intervalle unité [0, 1]. Le processus commence en retirant le quart médian de l'intervalle [0, 1]. L'ensemble résultat est donc Les étapes suivantes consistent à retirer des sous-intervalles de longueur 1/22n du milieu des 2n−1 intervalles restant. A la deuxième étape on retire donc (5/32, 7/32) and (25/32, 27/32) et l'ensemble résultat devient : Itérant cette règle à l'infini, l'ensemble de Smith–Volterra–Cantor est l'ensemble des points qui ne seront jamais retirés. L'image suivante illustre l'ensemble initial et cinq itérations. Par construction l'ensemble de Smith-Volterra-Cantor ne contient aucun intervalle. Or, durant le processus, on retire : Prouvant que l'ensemble des points restants est de mesure non nulle et égale à 1/2. Généralisation: En retirant rn de chaque sous-intervalle restant à l'itération n, l'ensemble résiduel aura une mesure positive si et seulement si la somme des termes de la suite est inférieure à la mesure de l'intervalle initial. Construction [modifier]
![left[0, frac{3}{8}right] cup left[frac{5}{8}, 1right].](http://upload.wikimedia.org/math/f/7/e/f7ef6cb7f76b048e2524b51eb48f24b0.png)
![left[0, frac{5}{32}right] cup left[frac{7}{32}, frac{3}{8}right] cup left[frac{5}{8}, frac{25}{32}right] cup left[frac{27}{32}, 1right].](http://upload.wikimedia.org/math/0/a/9/0a94caa89ba4a9178698a0dc81b4cff6.png)
Propriétés [modifier]
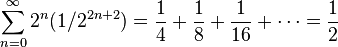
Voir aussi [modifier]
Liens externes [modifier]
11:37 Publié dans Ensemble de Smith-Volterra-Cantor | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook









































