02/12/2010
Algèbre de Lie
En mathématiques, une algèbre de Lie, nommée en l'honneur du mathématicien Sophus Lie, est un espace vectoriel qui est muni d'un crochet de Lie, c'est-à-dire d'une loi de composition interne bilinéaire, antisymétrique et qui vérifie l'identité de Jacobi. Une algèbre de Lie est un cas particulier d'algèbre sur un corps.Algèbre de Lie
Sommaire[masquer] |
Soit Une algèbre de Lie sur Le produit [x,y] est appelé crochet de Lie (ou simplement crochet) de x et y. Puisque le crochet est une fonction bilinéaire alternée de x,y, on a aussi l'identité [x,y] = − [y,x] pour tousx,y dans Une sous-algèbre de Lie de Remarque : contrairement aux algèbres tensorielles (et aux algèbres de Clifford, dont les algèbres extérieures), les algèbres de Lie ne sont pas unitaires, ni associatives. Un morphisme d'algèbre de Lie Un idéal de Si Une représentation d'une algèbre de Lie Le morphisme Les algèbres de Lie sont naturellement associées aux groupes de Lie. Si G est un groupe de Lie et 1 son élément neutre, alors l'espace tangent en 1 à G est une algèbre de Lie ; la construction exacte de cette algèbre est détaillée dans la section correspondante de l'article Groupe de Lie. La même construction est valable pour les groupes algébriques. On note en général en petites lettres gothiques l'algèbre de Lie associée à un groupe de Lie, ou à un groupe algébrique. Ainsi, comme on l'a déjà vu, Si φ est un morphisme de groupes entre deux groupes de Lie G et H, et si l'on suppose φ différentiable, alors sa différentielle en l'identité sera un morphisme entre les algèbres de Lie La classification des algèbres de Lie est utilisée de façon cruciale pour l'étude des groupes de Lie, des groupes algébriques et de leurs représentations. Si Une algèbre de Lie est dite nilpotente lorsque toute suite de commutateurs Plus précisément, définissons Ci par S'il existe un i tel que Ci=0, on dit que L'algèbre Le théorème d'Engel affirme que toute sous-algèbre nilpotente de Définissons par récurrence Di par S'il existe un i tel que Di=0, on dit que Un exemple d'algèbre de Lie résoluble est donné par l'algèbre Le théorème de Lie montre que, si On dit qu'une algèbre de Lie Lorsque On peut montrer que, sous les mêmes hypothèses, toute algèbre de Lie semi-simple est en fait une somme directe d'algèbres de Lie simples. Les algèbres de Lie simples de dimension finie sur le corps L'algèbre de Lie Les algèbres de Lie semi-simples de dimension finie sur le corps EI, EII, EIII, EIV (de type E6) EV, EVI, EVII (de type E7) EVIII, EIX (de type E8) FI, FII (de type F4) et GI (de type G2) suivant la notation d'Helgason1) Il n'y a pas de classification générale des algèbres de Lie de dimension infinie mais plusieurs classes de telles algèbres ont été étudiées. Il existe différentes sortes de généralisations des algèbres de Lie, on citera les superalgèbres de Lie, les groupes quantiques, les algèbres de Leibniz, les algèbres pré-Lie.Définitions, exemples et premières propriétés [modifier]
Définition [modifier]
 un corps.
un corps. est un espace vectoriel
est un espace vectoriel  sur
sur  muni d'une application bilinéaire
muni d'une application bilinéaire ![(x,y) mapsto [x,y]](http://upload.wikimedia.org/math/7/5/e/75e87350f83275e11f126171780fd7ca.png) de
de 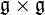 dans
dans  qui vérifie les propriétés suivantes:
qui vérifie les propriétés suivantes:
![forall x in mathfrak{g}, [x,x]=0](http://upload.wikimedia.org/math/f/3/2/f3223a3fe063412bb2f5033ba34850f5.png) ;
;![forall x,y,z in mathfrak{g}, [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0](http://upload.wikimedia.org/math/6/7/d/67d115952cf9c1c691b6053868febb0d.png)
 . L'identité (2) ci-dessus est appelée l'identité de Jacobi.
. L'identité (2) ci-dessus est appelée l'identité de Jacobi. est un sous-espace vectoriel de
est un sous-espace vectoriel de  stable pour le crochet de Lie. Toute sous-algèbre de Lie de
stable pour le crochet de Lie. Toute sous-algèbre de Lie de  est munie de manière évidente d'une structure d'algèbre de Lie sur
est munie de manière évidente d'une structure d'algèbre de Lie sur  .
.Quelques exemples classiques d'algèbres de Lie [modifier]
![forall x,y in E, [x,y]=0](http://upload.wikimedia.org/math/4/7/b/47b2e0b6393e77c2e6376834f8c87276.png) . Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne.
. Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne.![forall x,y in A, [x,y]=x*y-y*x](http://upload.wikimedia.org/math/5/9/7/59711ef28af13f749a361b567295a858.png) (c'est lecommutateur des deux éléments x et y). Il est facile de vérifier que l'on définit ainsi sur A une structure d'algèbre de Lie.
(c'est lecommutateur des deux éléments x et y). Il est facile de vérifier que l'on définit ainsi sur A une structure d'algèbre de Lie. est contenue dans une algèbre associative, appelée algèbre enveloppante, dans laquelle le crochet de Lie coïncide avec le crochet définit ci-dessus. L'algèbre enveloppante est beaucoup plus grande que l'algèbre de départ.
est contenue dans une algèbre associative, appelée algèbre enveloppante, dans laquelle le crochet de Lie coïncide avec le crochet définit ci-dessus. L'algèbre enveloppante est beaucoup plus grande que l'algèbre de départ. , l'espace des matrices
, l'espace des matrices 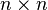 à coefficients dans
à coefficients dans  . C'est une algèbre associative pour le produit matriciel usuel. On peut donc également lui donner une structure d'algèbre de Lie, avec le crochet [A,B] = AB − BA. On note
. C'est une algèbre associative pour le produit matriciel usuel. On peut donc également lui donner une structure d'algèbre de Lie, avec le crochet [A,B] = AB − BA. On note  cette algèbre, lorsque l'on considère sa structure d'algèbre de Lie.
cette algèbre, lorsque l'on considère sa structure d'algèbre de Lie. stable par le crochet est une algèbre de Lie. Ainsi, on peut vérifier que l'ensemble des matrices de trace nulle est une algèbre de Lie, que l'on note
stable par le crochet est une algèbre de Lie. Ainsi, on peut vérifier que l'ensemble des matrices de trace nulle est une algèbre de Lie, que l'on note  .
. .
. avec le produit vectoriel comme crochet de Lie est une algèbre de Lie.
avec le produit vectoriel comme crochet de Lie est une algèbre de Lie.Morphismes et idéaux [modifier]
 est une application linéaire φ qui respecte le crochet de Lie, c'est-à-dire telle que
est une application linéaire φ qui respecte le crochet de Lie, c'est-à-dire telle que![forall a,b in mathfrak{g}, phi([a,b])=[phi(a),phi(b)]](http://upload.wikimedia.org/math/7/9/f/79fe9d02198bb8da7ba2c3fe5df52add.png) .
. est un sous-espace vectoriel
est un sous-espace vectoriel  tel que
tel que ![forall ginmathfrak{g}, forall hin mathfrak{h}, [g,h]inmathfrak{h}](http://upload.wikimedia.org/math/9/f/e/9fe5cc6e32f7a61a988f42d549cb43b3.png) . C'est en particulier une sous-algèbre de Lie. Si une algèbre de Lie n'admet pas d'idéal non trivial, elle est dite simple.
. C'est en particulier une sous-algèbre de Lie. Si une algèbre de Lie n'admet pas d'idéal non trivial, elle est dite simple. est un idéal de
est un idéal de  , on peut former le quotient de
, on peut former le quotient de  par
par  : c'est l'espace vectoriel quotient
: c'est l'espace vectoriel quotient 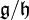 , muni du crochet défini par
, muni du crochet défini par ![[g+mathfrak{h},g'+mathfrak{h}] = [g,g']](http://upload.wikimedia.org/math/8/2/d/82d29f5c4eb7af6feb2661af74a7bd29.png) . La projection
. La projection 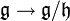 est alors un morphisme d'algèbres de Lie.
est alors un morphisme d'algèbres de Lie. est un morphisme
est un morphisme 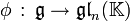 . Autrement dit, c'est une application linéaire telle que φ([g,h]) = φ(g)φ(h) − φ(h)φ(g).
. Autrement dit, c'est une application linéaire telle que φ([g,h]) = φ(g)φ(h) − φ(h)φ(g). défini par ad(g)(h) = [g,h] définit une représentation de
défini par ad(g)(h) = [g,h] définit une représentation de  , appelée représentation adjointe. L'identité de Jacobi exprime précisément le fait que ad respecte le crochet. Le noyau de cette représentation est le centre
, appelée représentation adjointe. L'identité de Jacobi exprime précisément le fait que ad respecte le crochet. Le noyau de cette représentation est le centre ![Z(mathfrak{g})={ginmathfrak{g}forall hinmathfrak{g} [g,h]=0}](http://upload.wikimedia.org/math/a/f/e/afe7160b530a847134d5f4291027ee9c.png) de l'algèbre de Lie
de l'algèbre de Lie 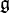 .
.Relation avec les groupes de Lie et les groupes algébriques [modifier]
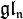 désigne l'ensemble des matrices carrées de taille n et
désigne l'ensemble des matrices carrées de taille n et 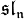 désigne l'ensemble des matrices carrées de taille n de trace nulle. De la même façon,
désigne l'ensemble des matrices carrées de taille n de trace nulle. De la même façon,  désigne l'ensemble des matrices carrées A de taille n antisymétriques, etc. Dans tous ces exemples, le crochet de Lie n'est rien d'autre que le commutateur : [A,B]=AB-BA.
désigne l'ensemble des matrices carrées A de taille n antisymétriques, etc. Dans tous ces exemples, le crochet de Lie n'est rien d'autre que le commutateur : [A,B]=AB-BA. et
et  de G et H. En particulier, à une représentation de G différentiable, on associe une représentation de
de G et H. En particulier, à une représentation de G différentiable, on associe une représentation de  .
.Classification [modifier]
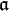 et
et 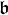 sont deux sous-algèbres de Lie d'une algèbre de Lie
sont deux sous-algèbres de Lie d'une algèbre de Lie  , notons
, notons ![[mathfrak{a},mathfrak{b}]](http://upload.wikimedia.org/math/c/5/2/c528d5c197e3f72db0a9bbc760333ee4.png) le sous-espace vectoriel engendré par les éléments de la forme [a,b] pour
le sous-espace vectoriel engendré par les éléments de la forme [a,b] pour  et
et 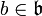 .
.Algèbres de Lie nilpotentes [modifier]
![[[[g_1,g_2],g_3],dots,g_n]](http://upload.wikimedia.org/math/4/8/a/48ab7757f1f2f8ed370a0f9d8acecd13.png) finit par être nulle, lorsque n devient suffisamment grand.
finit par être nulle, lorsque n devient suffisamment grand. et
et ![C_{i+1}=[C_i,mathfrak{g}]](http://upload.wikimedia.org/math/3/b/2/3b21f80fad4a73cdcc2c55569abfd0d0.png) .
. est nilpotente. Cette notion est à mettre en parallèle avec celle de groupe nilpotent. Il est facile de voir que toute algèbre de Lie abélienne est nilpotente.
est nilpotente. Cette notion est à mettre en parallèle avec celle de groupe nilpotent. Il est facile de voir que toute algèbre de Lie abélienne est nilpotente. des matrices triangulaires strictes, c'est-à-dire de la forme
des matrices triangulaires strictes, c'est-à-dire de la forme  fournit un exemple d'algèbre de Lie nilpotente.
fournit un exemple d'algèbre de Lie nilpotente. est en fait simultanément trigonalisable et donc conjuguée à une sous-algèbre de
est en fait simultanément trigonalisable et donc conjuguée à une sous-algèbre de  .
.Algèbres de Lie résolubles [modifier]
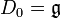 et Di + 1 = [Di,Di]
et Di + 1 = [Di,Di] est résoluble. Comme dans le cas des algèbres nilpotentes, cette notion correspond à celle de groupe résoluble. Il est facile de voir que toute algèbre de Lie nilpotente est résoluble.
est résoluble. Comme dans le cas des algèbres nilpotentes, cette notion correspond à celle de groupe résoluble. Il est facile de voir que toute algèbre de Lie nilpotente est résoluble.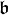 des matrices triangulaires supérieures dans
des matrices triangulaires supérieures dans  .
.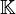 est algébriquement clos et de caractéristique nulle, alors toute sous-algèbre de Lie résoluble de
est algébriquement clos et de caractéristique nulle, alors toute sous-algèbre de Lie résoluble de  est conjuguée à une sous-algèbre de
est conjuguée à une sous-algèbre de 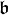
Algèbres de Lie semi-simples et réductives [modifier]
 est semi-simple lorsqu'elle ne contient pas d'idéal résoluble non trivial.
est semi-simple lorsqu'elle ne contient pas d'idéal résoluble non trivial.  est dite réductive lorsque sa représentation adjointe est semi-simple.
est dite réductive lorsque sa représentation adjointe est semi-simple.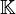 est de caractéristique nulle, et que
est de caractéristique nulle, et que  est de dimension finie, la semi-simplicité de
est de dimension finie, la semi-simplicité de  est équivalente à la non-dégénerescence de la forme de Killing K(x,y) définie par K(x,y) = tr(ad(x)ad(y)), où tr désigne la trace. Par ailleurs,
est équivalente à la non-dégénerescence de la forme de Killing K(x,y) définie par K(x,y) = tr(ad(x)ad(y)), où tr désigne la trace. Par ailleurs,  est réductive si et seulement si
est réductive si et seulement si ![[mathfrak{g},mathfrak{g}]](http://upload.wikimedia.org/math/3/f/1/3f1683bcf0fa96e29329efca70a1d284.png) est semi-simple.
est semi-simple. des nombres complexes sont classifiées par les diagrammes de Dynkin. Il y a donc 4 familles d'algèbres de Lie simples (ou 3 si on considère Bn et Dn comme une même famille) et 5 algèbres de Lie exceptionnelles, correspondant chacune à un diagramme de Dynkin différent.
des nombres complexes sont classifiées par les diagrammes de Dynkin. Il y a donc 4 familles d'algèbres de Lie simples (ou 3 si on considère Bn et Dn comme une même famille) et 5 algèbres de Lie exceptionnelles, correspondant chacune à un diagramme de Dynkin différent.
 correspond l'algèbre de Lie
correspond l'algèbre de Lie 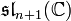 .
.
 correspond l'algèbre de Lie
correspond l'algèbre de Lie 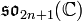 .
.
 correspond l'algèbre de Lie
correspond l'algèbre de Lie  .
.
 correspond l'algèbre de Lie
correspond l'algèbre de Lie  .
.
 est, elle, réductive et son algèbre de Lie dérivée est
est, elle, réductive et son algèbre de Lie dérivée est 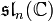 .
. des nombres réels sont classifiées par les involutions d'algèbres de Lie complexe ou, de façon équivalente, par lesinvolutions de systèmes de racines. Ceci correspond à la notion d'algèbre de Lie symétrique. Comme classe d'algèbre de Lie simple réelle, on peut citer:
des nombres réels sont classifiées par les involutions d'algèbres de Lie complexe ou, de façon équivalente, par lesinvolutions de systèmes de racines. Ceci correspond à la notion d'algèbre de Lie symétrique. Comme classe d'algèbre de Lie simple réelle, on peut citer:
Dimension infinie [modifier]
Généralisation [modifier]
Références [modifier]
Voir aussi [modifier]
21:26 Publié dans Algèbre de Lie | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook








































